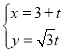题目内容
【题目】已知椭圆
的离心率
，过焦点且垂直于x轴的直线被椭圆截得的线段长为3
（1）求椭圆的方程；
（2）已知P为直角坐标平面内一定点，动直线l：
与椭圆交于A、B两点，当直线PA与直线PB的斜率均存在时，若直线PA与PB的斜率之和为与t无关的常数，求出所有满足条件的定点P的坐标.
【答案】(1) 
.(2) 
或
.
【解析】
（1）由题意求得a，c的值，结合隐含条件求得b，则椭圆方程可求；
（2）设
，
，
，将
代入椭圆方程，利用韦达定理及斜率公式化简可得
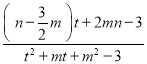，与t无关，由此能求出存在满足条件的m，n的值．
（1）设椭圆的半焦距为
，则
，且
.
由
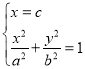，解得
.
依题意，
，求得c=1，
，
，于是椭圆的方程为.
（2）设，，，将：
代入椭圆方程得
.
，
，
则有
，
.
直线
，
的斜率之和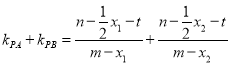
，
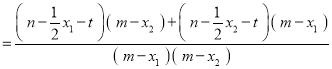
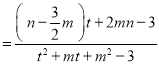当
，
时斜率的和恒为0，
解得
或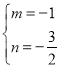
.
综上所述，所有满足条件的定点
的坐标为
或
.
练习册系列答案
名校课堂系列答案
相关题目
