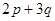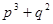题目内容
设不等式 的解集为A,且
的解集为A,且
(Ⅰ)求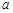 的值
的值
(Ⅱ)求函数 的最小值
的最小值
 的解集为A,且
的解集为A,且
(Ⅰ)求
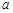 的值
的值(Ⅱ)求函数
 的最小值
的最小值(Ⅰ)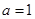 (Ⅱ)
(Ⅱ)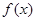 的最小值为
的最小值为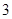
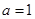 (Ⅱ)
(Ⅱ)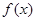 的最小值为
的最小值为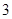
(Ⅰ)因为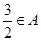 ,且
,且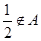 ,所以
,所以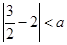 ,且
,且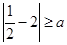
解得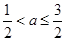 ,又因为
,又因为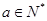 ,所以
,所以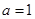
(Ⅱ)因为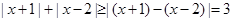
当且仅当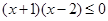 ,即
,即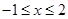 时取得等号,所以
时取得等号,所以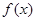 的最小值为
的最小值为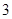
不等式选讲如果如此题只考查绝对值不等式就算比较容易的题目,注意绝对值的三角不等式即可,当然也可通过讨论去掉绝对值号,当然还要注意均值和柯西不等式的应用。
【考点定位】本题考查绝对值不等式的基本内容,属于简单题。
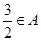 ,且
,且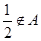 ,所以
,所以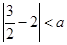 ,且
,且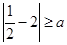
解得
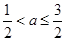 ,又因为
,又因为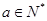 ,所以
,所以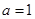
(Ⅱ)因为
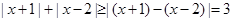
当且仅当
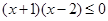 ,即
,即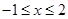 时取得等号,所以
时取得等号,所以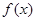 的最小值为
的最小值为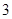
不等式选讲如果如此题只考查绝对值不等式就算比较容易的题目,注意绝对值的三角不等式即可,当然也可通过讨论去掉绝对值号,当然还要注意均值和柯西不等式的应用。
【考点定位】本题考查绝对值不等式的基本内容,属于简单题。

练习册系列答案
相关题目
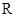 上的偶函数,
上的偶函数,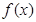 满足
满足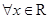 ,都有
,都有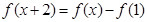 ,且当
,且当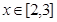 时,
时,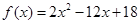 .若函数
.若函数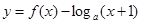 在
在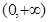 上有三个零点,则
上有三个零点,则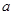 的取值范围是 .
的取值范围是 .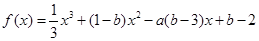 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是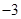 ,则不等式组
,则不等式组 所确定的平面区域在
所确定的平面区域在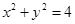 内的面积为 ( )
内的面积为 ( )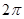
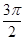
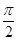
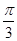
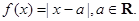
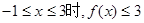 ,求
,求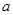 的取值范围;
的取值范围;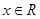 ,
,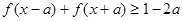 恒成立,求实数
恒成立,求实数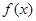 的定义域为R,最小正周期
的定义域为R,最小正周期 ,若
,若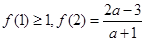 ,则
,则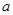 的取值范围是
的取值范围是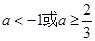
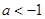

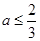
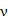 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度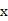 (单位:辆/千米)的函数。当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时。研究表明当
(单位:辆/千米)的函数。当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时。研究表明当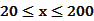 时,车流速度
时,车流速度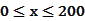 时,求函数
时,求函数 的表达式;
的表达式;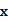 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)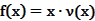 可以达到最大?并求出最大值。(精确到1辆/小时)
可以达到最大?并求出最大值。(精确到1辆/小时)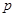 ,
, 那么
那么 等于( )
等于( )