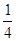题目内容
设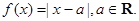
(1)当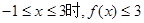 ,求
,求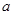 的取值范围;
的取值范围;
(2)若对任意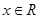 ,
,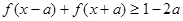 恒成立,求实数
恒成立,求实数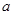 的最小值.
的最小值.
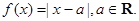
(1)当
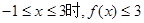 ,求
,求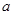 的取值范围;
的取值范围;(2)若对任意
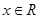 ,
,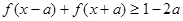 恒成立,求实数
恒成立,求实数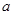 的最小值.
的最小值.(1)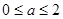 ,(2)
,(2)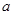 的最小值为
的最小值为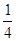
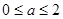 ,(2)
,(2)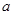 的最小值为
的最小值为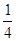
试题分析:根据题意,由于
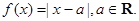 那么可知当
那么可知当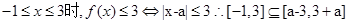 ,故可知参数a的范围是
,故可知参数a的范围是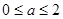
(2)对于对任意
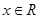 ,
,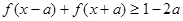 恒成立则可知为
恒成立则可知为 即可,那么求解可知参数a 最小值为
即可,那么求解可知参数a 最小值为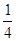
点评:主要是考查了绝对值不等式的求解的运用,属于基础题。

练习册系列答案
相关题目
题目内容
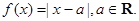
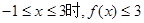 ,求
,求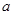 的取值范围;
的取值范围;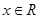 ,
,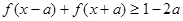 恒成立,求实数
恒成立,求实数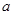 的最小值.
的最小值.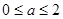 ,(2)
,(2)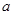 的最小值为
的最小值为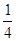
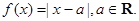 那么可知当
那么可知当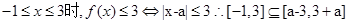 ,故可知参数a的范围是
,故可知参数a的范围是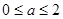
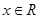 ,
,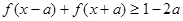 恒成立则可知为
恒成立则可知为 即可,那么求解可知参数a 最小值为
即可,那么求解可知参数a 最小值为