ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥–ΘΗΏΕΰΘ®20Θ©ΑύΙ≤50Οϊ―ß…ζΘ§‘ΎΤΎ÷–ΩΦ ‘÷–Θ§ΟΩΈΜΆ§―ßΒΡ ΐ―ßΩΦ ‘Ζ÷ ΐΕΦ‘Ύ«χΦδ![]() ΡΎΘ§ΫΪΗΟΑύΥυ”–Ά§―ßΒΡΩΦ ‘Ζ÷ ΐΖ÷ΈΣΤΏΗωΉιΘΚ
ΡΎΘ§ΫΪΗΟΑύΥυ”–Ά§―ßΒΡΩΦ ‘Ζ÷ ΐΖ÷ΈΣΤΏΗωΉιΘΚ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§Μφ÷Τ≥ωΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ»γΆΦΥυ Ψ.
Θ§Μφ÷Τ≥ωΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ»γΆΦΥυ Ψ.

Θ®1Θ©ΗυΨίΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§ΙάΦΤ’β¥ΈΩΦ ‘―ß…ζ≥…Φ®ΒΡ÷–ΈΜ ΐΚΆΤΫΨυ ΐΘΜ
Θ®2Θ©“―÷Σ≥…Φ®ΈΣ104Ζ÷Μρ105Ζ÷ΒΡΆ§―ßΙ≤”–3»ΥΘ§œ÷¥”≥…Φ®‘Ύ![]() ÷–ΒΡΆ§―ß÷–»Έ―Γ2»ΥΘ§‘ρ÷Ν…Ό”–1»Υ≥…Φ®≤ΜΒΆ”Ύ106Ζ÷ΒΡΗ≈¬ ΈΣΕύ…ΌΘΩΘ®ΟΩΈΜΆ§―ßΒΡ≥…Φ®ΕΦΈΣ’ϊ ΐΘ©
÷–ΒΡΆ§―ß÷–»Έ―Γ2»ΥΘ§‘ρ÷Ν…Ό”–1»Υ≥…Φ®≤ΜΒΆ”Ύ106Ζ÷ΒΡΗ≈¬ ΈΣΕύ…ΌΘΩΘ®ΟΩΈΜΆ§―ßΒΡ≥…Φ®ΕΦΈΣ’ϊ ΐΘ©
ΓΨ¥πΑΗΓΩΘ®1Θ©÷–ΈΜ ΐΈΣ114Θ§ΤΫΨυ ΐΈΣ114.32ΘΜΘ®2Θ©![]()
ΓΨΫβΈωΓΩ
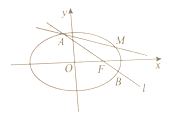
Θ®ΔώΘ©ΗυΨί÷–ΈΜ ΐΒΡΝΫ±ΏΗ≈¬ œύΒ»Θ§Φ¥Ω…«σ≥ω÷–ΈΜ ΐΘΜ”…ΟΩΉιΒΡ÷–Φδ÷Β≥Υ“‘ΗΟΉιΒΡΤΒ¬ ‘Ό«σΚΆΦ¥Ω…«σ≥ωΤΫΨυ ΐΘΜ
Θ®ΔρΘ©œ»”…Χβ“β«σ≥ω≥…Φ®‘Ύ![]() ΒΡ»Υ ΐΘ§Ε‘≥…Φ®ΈΣ104Ζ÷Μρ105Ζ÷ΒΡΆ§―ßΚΆ≥…Φ®ΈΣ106Ζ÷ΓΔ107Ζ÷ΒΡ―ß…ζ±ύΚ≈Θ§”ΟΝ–ΨΌΖ®ΫαΚœΙ≈ΒδΗ≈–ΆΒΡΗ≈¬ ΦΤΥψΙΪ ΫΦ¥Ω…«σ≥ωΫαΙϊ.
ΒΡ»Υ ΐΘ§Ε‘≥…Φ®ΈΣ104Ζ÷Μρ105Ζ÷ΒΡΆ§―ßΚΆ≥…Φ®ΈΣ106Ζ÷ΓΔ107Ζ÷ΒΡ―ß…ζ±ύΚ≈Θ§”ΟΝ–ΨΌΖ®ΫαΚœΙ≈ΒδΗ≈–ΆΒΡΗ≈¬ ΦΤΥψΙΪ ΫΦ¥Ω…«σ≥ωΫαΙϊ.
Θ®ΔώΘ©”…ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§÷Σ![]() Θ§Υυ“‘―ß…ζ≥…Φ®ΒΡ÷–ΈΜ ΐΈΣ
Θ§Υυ“‘―ß…ζ≥…Φ®ΒΡ÷–ΈΜ ΐΈΣ![]() .
.
ΤΫΨυ ΐΈΣ![]()
![]() .
.
Θ®ΔρΘ©“ρΈΣ![]() Θ§Υυ“‘≥…Φ®‘Ύ
Θ§Υυ“‘≥…Φ®‘Ύ![]() ÷°ΦδΒΡ―ß…ζΙ≤”–6»Υ.
÷°ΦδΒΡ―ß…ζΙ≤”–6»Υ.
…η≥…Φ®ΈΣ104Ζ÷ΓΔ105Ζ÷ΒΡ―ß…ζΈΣ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§≥…Φ®ΈΣ106Ζ÷ΓΔ107Ζ÷ΒΡ―ß…ζΈΣ
Θ§≥…Φ®ΈΣ106Ζ÷ΓΔ107Ζ÷ΒΡ―ß…ζΈΣ![]() Θ§
Θ§![]() Θ§
Θ§![]() .¥”6»Υ÷–»Έ―Γ2»ΥΘ§Ι≤”–
.¥”6»Υ÷–»Έ―Γ2»ΥΘ§Ι≤”–![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() 15÷÷«ιΩωΘ§Τδ÷–«ΓΚΟ2»ΥΕΦ≤ΜΒΆ”Ύ106Ζ÷ΒΡ”–
15÷÷«ιΩωΘ§Τδ÷–«ΓΚΟ2»ΥΕΦ≤ΜΒΆ”Ύ106Ζ÷ΒΡ”–![]() Θ§
Θ§![]() Θ§
Θ§![]() Ι≤3÷÷«ιΩωΘ§Τδ÷–”–1»Υ≤ΜΒΆ”Ύ106Ζ÷1»ΥΒΆ”Ύ106Ζ÷ΒΡ”–
Ι≤3÷÷«ιΩωΘ§Τδ÷–”–1»Υ≤ΜΒΆ”Ύ106Ζ÷1»ΥΒΆ”Ύ106Ζ÷ΒΡ”–![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Ι≤9»ΥΘ§Υυ“‘¥”≥…Φ®‘Ύ
Ι≤9»ΥΘ§Υυ“‘¥”≥…Φ®‘Ύ![]() ÷–ΒΡΆ§―ß÷–»Έ―Γ2»ΥΘ§‘ρ÷Ν…Ό”–1»Υ≥…Φ®ΕΦ≤ΜΒΆ”Ύ106Ζ÷ΒΡΗ≈¬ ΈΣ
÷–ΒΡΆ§―ß÷–»Έ―Γ2»ΥΘ§‘ρ÷Ν…Ό”–1»Υ≥…Φ®ΕΦ≤ΜΒΆ”Ύ106Ζ÷ΒΡΗ≈¬ ΈΣ![]() .
.

ΓΨΧβΡΩΓΩΈΣ±ΘΜΛ≈©Οώ÷÷ΝΗ ’“φΘ§¥ΌΫχΝΗ ≥…ζ≤ζΘ§»Ζ±ΘΙζΦ“ΝΗ ≥Α≤»ΪΘ§ΒςΕ·Ιψ¥σ≈©ΟώΝΗ ≥…ζ≤ζΒΡΜΐΦΪ–‘Θ§¥”2004ΡξΩΣ ΦΘ§ΙζΦ“ Β ©ΝΥΕ‘÷÷ΝΗ≈©Οώ÷±Ϋ”≤ΙΧυ.Ά®ΙΐΕ‘2014ΓΪ2018ΡξΒΡ ΐΨίΫχ––Βς≤ιΘ§ΖΔœ÷Ρ≥ΒΊ«χΖΔΖ≈ΝΗ ≥≤ΙΧυΕν![]() Θ®“Ύ‘ΣΘ©”κΗΟΒΊ«χΝΗ ≥≤ζΝΩ
Θ®“Ύ‘ΣΘ©”κΗΟΒΊ«χΝΗ ≥≤ζΝΩ![]() Θ®Άρ“ΎΕ÷Θ©÷°Φδ¥φ‘ΎΉ≈œΏ–‘œύΙΊΙΊœΒ.Ά≥ΦΤ ΐΨί»γœ¬±μΘΚ
Θ®Άρ“ΎΕ÷Θ©÷°Φδ¥φ‘ΎΉ≈œΏ–‘œύΙΊΙΊœΒ.Ά≥ΦΤ ΐΨί»γœ¬±μΘΚ
ΡξΖί | 2014Ρξ | 2015Ρξ | 2016Ρξ | 2017Ρξ | 2018Ρξ |
≤ΙΧυΕν | 9 | 10 | 12 | 11 | 8 |
ΝΗ ≥≤ζΝΩ | 23 | 25 | 30 | 26 | 21 |
Θ®1Θ©«κΗυΨί»γ±μΥυΗχΒΡ ΐΨίΘ§«σ≥ω![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡœΏ–‘ΜΊΙι÷±œΏΖΫ≥Χ
ΒΡœΏ–‘ΜΊΙι÷±œΏΖΫ≥Χ![]() ΘΜ
ΘΜ
Θ®2Θ©Ά®ΙΐΕ‘ΗΟΒΊ«χΝΗ ≥≤ζΝΩΒΡΖ÷Έω―–ΨΩΘ§ΦΤΜ°2019Ρξ‘ΎΗΟΒΊ«χΖΔΖ≈ΝΗ ≥≤ΙΧυΕν7“Ύ‘ΣΘ§«κΗυΨίΘ®1Θ©÷–ΥυΒΟΒΡœΏ–‘ΜΊΙι÷±œΏΖΫ≥ΧΘ§‘Λ≤β2019ΡξΗΟΒΊ«χΒΡΝΗ ≥≤ζΝΩ.
Θ®≤ΈΩΦΙΪ ΫΘΚ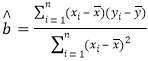 Θ§
Θ§![]() Θ©
Θ©