Question

【题目】设函数，则下列命题中正确的个数是（ ）

①当时，函数在上有最小值；②当时，函数在是单调增函数；③若，则；④方程可能有三个实数根.

A.1B.2C.3D.4

Answer 1

【答案】C

【解析】

①当b＞0时，把函数f（x）＝|x|x-bx+c分x≥0和x＜0两种情况讨论，转化为二次函数判单调性，求最值即可；

②当b＜0时，判断f（x）在和是单调增函数加以判断；

③推导f（x）+ f（-x）＝2c即可求解；

④对b，c取特值求方程f（x）＝0有三个实数根，故可判断．

①当b＞0时，f（x）＝|x|x-bx+c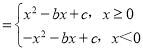，知函数f（x）在上是单调减函数,在， 上是单调增函数,故函数在上无最小值；故①错误；

②当b＜0时，由①知函数f（x）在和是单调增函数,且函数在处连续，则在是单调增函数；故②正确；

③f（x）+ f（-x）＝2c,故若，则；故③正确

④令b＝3，c＝2，则f（x）＝|x|x﹣3x+2＝0，解得x＝1，2， ．故④正确．

故正确的为②③④．

故选：C