题目内容
【题目】已知函数![]() .
.
(1)已知f(x)的图象关于原点对称,求实数![]() 的值;
的值;
(2)若![]() ,已知常数
,已知常数![]() 满足:
满足:![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题(1)函数![]() 的定义域是
的定义域是![]() ,函数图象关于原点对称,得函数
,函数图象关于原点对称,得函数![]() 是奇函数,即
是奇函数,即![]() 解出即可,需验证函数
解出即可,需验证函数![]() 是奇函数;(2)此题是个恒成立问题,求取参量的取值范围,对此我们一般情况都是参变分离,化成
是奇函数;(2)此题是个恒成立问题,求取参量的取值范围,对此我们一般情况都是参变分离,化成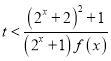 ,令
,令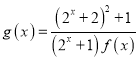 ,由于是恒成立问题,则有
,由于是恒成立问题,则有![]() ,只需要求取
,只需要求取![]() 即可.
即可.
试题解析:(1)定义域为![]() ,又知函数为R上的奇函数,则
,又知函数为R上的奇函数,则![]()
![]() a=
a=![]()
下面证明![]()
![]() 时
时![]() 是奇函数
是奇函数
![]()
对定义域R上的每一个x都成立,
∴![]() 为R上的奇函数.
为R上的奇函数.
∴存在实数![]() ,使函数
,使函数![]() 为奇函数.
为奇函数.
另解:定义域为![]() ,又知函数为R上的奇函数,
,又知函数为R上的奇函数,
![]() 对
对![]() 定义域R上的每一个x都成立.
定义域R上的每一个x都成立.
∴![]()
∴![]()
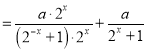
![]()
![]() =
=![]() ,
,
∴![]() .
.
∴存在实数![]() ,使函数
,使函数![]() 为奇函数.
为奇函数.
(2)若![]() ,则
,则![]() ,
,
![]() ,
,
由![]() 对
对![]() 恒成立,得
恒成立,得![]() ,
,
∵当![]() 时,
时,![]() ,
,
∴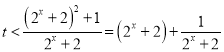 对
对![]() 恒成立,
恒成立,
易知,关于x的函数![]() 在上
在上![]() 为增函数,令
为增函数,令![]()
![]() 在
在![]() 上为增,
上为增,![]()
∴![]() .
.

练习册系列答案
相关题目
【题目】从某食品厂生产的面包中抽取![]() 个,测量这些面包的一项质量指标值,由测量结果得如下频数分布表:
个,测量这些面包的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 |
|
|
|
|
|
频数 |
|
|
|
|
|

(1)在相应位置上作出这些数据的频率分布直方图;
(2)估计这种面包质量指标值的平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(3)根据以上抽样调查数据,能否认为该食品厂生产的这种面包符合“质量指标值不低于![]() 的面包至少要占全部面包
的面包至少要占全部面包![]() 的规定?”
的规定?”
【题目】某地通过市场调查得到西红柿种植成本![]() (单位:元/千克)与上市时间
(单位:元/千克)与上市时间![]() (单位:
(单位:![]() 天)的数据如下表:
天)的数据如下表:
时间 |
|
|
|
种植成本 |
|
|
|
(1)根据上表数据,发现二次函数能够比较准确描述![]() 与
与![]() 的变化关系,请求出函数的解析式;
的变化关系,请求出函数的解析式;
(2)利用选取的函数,求西红柿最低种植成本及此时的上市天数.