题目内容
4. 如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,则$\frac{|NB|}{|NA|}$-$\frac{|MA|}{|MB|}$=2.
如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,则$\frac{|NB|}{|NA|}$-$\frac{|MA|}{|MB|}$=2.
分析 先求出C的坐标,再设M(cosα,sinα),N(cosβ,sinβ),即可求出$\frac{|NB|}{|NA|}$-$\frac{|MA|}{|MB|}$.
解答 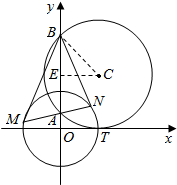 解:∵圆C与x轴相切于点T(1,0),
解:∵圆C与x轴相切于点T(1,0),
∴圆心的横坐标x=1,取AB的中点E,
∵|AB|=2,∴|BE|=1,
则|BC|=$\sqrt{2}$,即圆的半径r=|BC|=$\sqrt{2}$,
∴圆心C(1,$\sqrt{2}$),
∴E(0,$\sqrt{2}$),
又∵|AB|=2,且E为AB中点,
∴A(0,$\sqrt{2}$-1),B(0,$\sqrt{2}$+1),
∵M、N在圆O:x2+y2=1上,
∴可设M(cosα,sinα),N(cosβ,sinβ),
∴|NA|=$\sqrt{(cosβ-0)^{2}+[sinβ-(\sqrt{2}-1)^{2}}$=$\sqrt{2(\sqrt{2}-1)(\sqrt{2}-sinβ)}$,
|NB|=$\sqrt{(cosβ-0)^{2}+[sinβ-(\sqrt{2}+1)]^{2}}$=$\sqrt{2(\sqrt{2}+1)(\sqrt{2}-sinβ)}$,
∴$\frac{|NB|}{|NA|}$=$\sqrt{2}$+1,
同理可得$\frac{|MA|}{|MB|}$=$\sqrt{2}-1$,
∴$\frac{|NB|}{|NA|}$-$\frac{|MA|}{|MB|}$=2,
故答案为:2.
点评 本题考查求圆的标准方程,用三角函数值表示单位圆上点的坐标是解决本题的关键,注意解题方法的积累,属于难题.

练习册系列答案
相关题目
9.已知sinα+cosα=$\frac{1}{2}$,α∈(0,π),则$\frac{1-tanα}{1+tanα}$=( )
| A. | $\sqrt{7}$ | B. | -$\sqrt{7}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
16.已知i是虚数单位,则复数$\frac{1-2i}{1+2i}$=( )
| A. | -$\frac{3}{5}$-$\frac{4}{5}$i | B. | -$\frac{3}{5}$+$\frac{4}{5}$i | C. | $\frac{3}{5}$-$\frac{4}{5}$i | D. | $\frac{3}{5}$+$\frac{4}{5}$i |
13.已知f(x)=$\frac{1}{2}{x^2}+2x{f^'}({2015})+2015lnx$,则f′(2015)=( )
| A. | 2015 | B. | -2015 | C. | 2016 | D. | -2016 |