题目内容
【题目】如图,已知曲线![]() ,曲线
,曲线![]() ,
, ![]() 是平面上一点,若存在过点
是平面上一点,若存在过点![]() 的直线与
的直线与![]() 都有公共点,则称
都有公共点,则称![]() 为“
为“![]() 型点”.
型点”.

(1)证明: ![]() 的左焦点是“
的左焦点是“![]() 型点”;
型点”;
(2)设直线![]() 与
与![]() 有公共点,求证:
有公共点,求证: ![]() ,进而证明原点不是“
,进而证明原点不是“![]() 型点”;
型点”;
(3)求证: ![]() 内的点都不是“
内的点都不是“![]() 型点”.
型点”.
【答案】(1) ![]() ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
【解析】试题分析:(1)由题意![]() 的左焦点为
的左焦点为![]() ,过
,过![]() 的直线
的直线![]() 与
与![]() 、
、![]() 交于
交于![]() ,即可判定,得出直线方程;
,即可判定,得出直线方程;
(2)联立方程组![]() 和
和![]() ,根据方程有解,即可求解
,根据方程有解,即可求解![]() 的范围,从而判断原点不是“
的范围,从而判断原点不是“![]() 型点”;
型点”;
(3)以![]() 为边界的正方形区域记为
为边界的正方形区域记为![]() ,分点
,分点![]() 在
在![]() 的边界上,和
的边界上,和![]() 是区域
是区域![]() 内的点,两种情况分类讨论,进而说明
内的点,两种情况分类讨论,进而说明![]() ,联立方程组,得出
,联立方程组,得出![]() ,得出直线与曲线没有公共点,从而证得结论.
,得出直线与曲线没有公共点,从而证得结论.
试题解析:
(1)![]() 的左焦点为
的左焦点为![]() ,
,
过![]() 的直线
的直线![]() 与
与![]() 交于
交于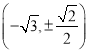 ,与
,与![]() 交于
交于![]() ,故
,故![]() 的左焦点为“
的左焦点为“![]() 型点”,且直线可以为
型点”,且直线可以为![]() ;
;
(2)直线![]() 与
与![]() 有交点,则
有交点,则![]() ,
,
若方程组有解,则必须![]() ;
;
直线![]() 与
与![]() 有交点,则
有交点,则![]() ,
,
若方程组有解,则必须![]()
故直线![]() 至多与曲线
至多与曲线![]() 和
和![]() 中的一条有交点,即原点不是“
中的一条有交点,即原点不是“![]() 型点”
型点”
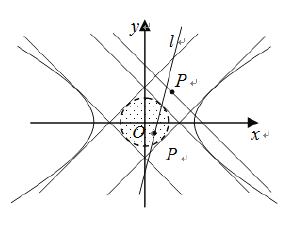
(3)以![]() 为边界的正方形区域记为
为边界的正方形区域记为![]() .
.
1)若点![]() 在
在![]() 的边界上,则该边所在直线与
的边界上,则该边所在直线与![]() 相切,与
相切,与![]() 有公共部分,即
有公共部分,即![]() 边界上的点都是“
边界上的点都是“![]() 型点”;
型点”;
2)设![]() 是区域
是区域![]() 内的点,即
内的点,即![]() ,
,
假设![]() 是“
是“![]() 型点”,则存在过点
型点”,则存在过点![]() 的直线
的直线![]() 与
与![]() 都有公共点.
都有公共点.
ⅰ)若直线![]() 与
与![]() 有公共点,直线
有公共点,直线![]() 的方程化为
的方程化为![]() ,假设
,假设![]() ,则
,则![]() ,
,
可知直线![]() 在
在![]() 之间,与
之间,与![]() 无公共点,这与“直线
无公共点,这与“直线![]() 与
与![]() 有公共点”矛盾,所以得到:与
有公共点”矛盾,所以得到:与![]() 有公共点的直线
有公共点的直线![]() 的斜率
的斜率![]() 满足
满足![]() .
.
ⅱ)假设![]() 与
与![]() 也有公共点,则方程组
也有公共点,则方程组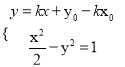 有实数解.
有实数解.
从方程组得![]() ,
,
![]() ,由
,由![]() ,
, ![]()
因为![]()
![]()
所以, ![]() ,即直线
,即直线![]() 与
与![]() 没有公共点,与“直线
没有公共点,与“直线![]() 与
与![]() 有公共点”矛盾,于是可知
有公共点”矛盾,于是可知![]() 不是“
不是“![]() 型点”.
型点”.
证明完毕
另解: ![]()
令![]() ,因为
,因为![]() ,所以|
,所以|![]() ,即
,即![]() .于是可知
.于是可知![]() 的图像是开口向下的抛物线,且对称轴方程为是
的图像是开口向下的抛物线,且对称轴方程为是![]() ,因为
,因为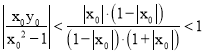 ,
,
所以![]() 在区间
在区间![]() 上为增函数,在
上为增函数,在![]() 上为减函数.
上为减函数.
因为![]() ,
, ![]() ,所以对任意
,所以对任意![]() ,都有
,都有![]() ,即直线
,即直线![]() 与
与![]() 没有公共点,与“直线
没有公共点,与“直线![]() 与
与![]() 有公共点”矛盾,于是可知
有公共点”矛盾,于是可知![]() 不是“
不是“![]() 型点”.
型点”.
证明完毕.