��Ŀ����
12����֪����p1������y=lntanx��y=$\frac{1}{2}$ln$\frac{1-cos2x}{1+cos2x}$��ͬһ������p2����֪x0�Ǻ���f��x��=$\frac{1}{1-x}$+2x��һ����㣬��1��x1��x0��x2����f��x1����0��f��x2���������������⣺��p1��p2���ڣ��Vp1���ģ��Vp2�����ۣ��Vp1����p2����p1�ţ��Vp2���У��������Ǣ٢ۣ�д��������ȷ�������ţ������� ���жϳ�����p1��p2����٣��Ӷ��жϳ������������ټ��ɣ�
��� �⣺��������p1������y=lntanx��y=$\frac{1}{2}$ln$\frac{1-cos2x}{1+cos2x}$��ͬһ������
���ں���y=$\frac{1}{2}$ln$\frac{1-cos2x}{1+cos2x}$=$\frac{1}{2}$lntan2x=ln$\sqrt{{tan}^{2}x}$��Ҫ��tanx��0��
������y=lntanx��Ҫ��tanx��0��
������p1�Ǽ����⣻
��������p2����֪x0�Ǻ���f��x��=$\frac{1}{1-x}$+2x��һ����㣬
��f��x��=0���ã�2x=$\frac{1}{x-1}$��
��g��x��=2x��h��x��=$\frac{1}{x-1}$��
��������g��x����h��x����ͼ����ͼʾ��
��ͼ��ã�
��1��x1��x0��x2����f��x1����0��f��x2����
������p2�������⣻
�ʴ�Ϊ���٢ۣ�
���� ���⿼�������Ǻ������������������ʡ����麯����������⣬���鸴��������жϣ���һ���е��⣮

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
2��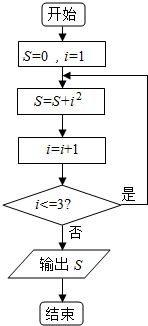 �Ķ���ͼ�ij����ͼ���������S=��������
�Ķ���ͼ�ij����ͼ���������S=��������
 �Ķ���ͼ�ij����ͼ���������S=��������
�Ķ���ͼ�ij����ͼ���������S=��������| A�� | 14 | B�� | 20 | C�� | 30 | D�� | 55 |
3��ֱ��x=-2����б�Ǻ�б�ʷֱ��ǣ�������
| A�� | 45�㣬1 | B�� | 135�㣬-1 | C�� | 90�㣬������ | D�� | 180�㣬������ |
7����ABC�У���A��B��C�ĶԱ߷ֱ�Ϊa��b��c�����ABC�����ΪS��S=$\frac{\sqrt{3}}{12}$��c2-a2-b2�������C���ڣ�������
| A�� | $\frac{��}{6}$ | B�� | $\frac{5��}{6}$ | C�� | $\frac{��}{3}$ | D�� | $\frac{2��}{3}$ |