题目内容
在平面直角坐标系xOy中,已知双曲线C:2x2-y2=1。
(1)设F是C的左焦点,M是C右支上一点,若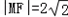 ,求点M的坐标;
,求点M的坐标;
(2)过C的左焦点作C的两条渐近线的平行线,求这两组平行线围成的平行四边形的面积;
(3)设斜率为k( )的直线l交C于P、Q两点,若l与圆x2+y2=1相切,求证:OP⊥OQ。
)的直线l交C于P、Q两点,若l与圆x2+y2=1相切,求证:OP⊥OQ。
(1)设F是C的左焦点,M是C右支上一点,若
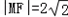 ,求点M的坐标;
,求点M的坐标;(2)过C的左焦点作C的两条渐近线的平行线,求这两组平行线围成的平行四边形的面积;
(3)设斜率为k(
 )的直线l交C于P、Q两点,若l与圆x2+y2=1相切,求证:OP⊥OQ。
)的直线l交C于P、Q两点,若l与圆x2+y2=1相切,求证:OP⊥OQ。解:(1)双曲线C1: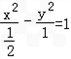 的左焦点F(-
的左焦点F(-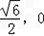 ),设M(x,y),
),设M(x,y),
则|MF|2=(x+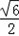 )2+y2,
)2+y2,
由M点是右支上的一点,可知x≥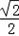 ,
,
所以|MF|=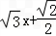 =2
=2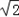 ,得x=
,得x=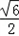 ,
,
所以M(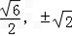 )。
)。
(2)左顶点A(-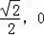 ),渐近线方程为:y=±
),渐近线方程为:y=±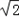 x
x
过A与渐近线y=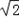 x平行的直线方程为y=
x平行的直线方程为y=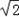 (x+
(x+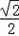 ),即y=
),即y=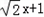 ,
,
所以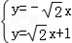 ,解得
,解得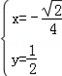
所以所求平行四边形的面积为S=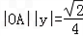 。
。
(2)设直线PQ的方程为y=kx+b,因直线PQ与已知圆相切,故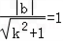 ,
,
即b2=k2+1…①,
由 ,得(2-k2)x2-2bkx-b2-1=0,
,得(2-k2)x2-2bkx-b2-1=0,
设P(x1,y1),Q(x2,y2),则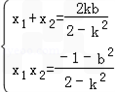 ,
,
又y1y2=(kx1+b)(kx2+b)
所以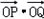 =x1x2+y1y2=(1+k2)x1x2+kb(x1+x2)+b2=
=x1x2+y1y2=(1+k2)x1x2+kb(x1+x2)+b2=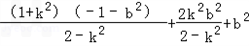 =
=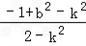
由①式可知 ,故PO⊥OQ。
,故PO⊥OQ。
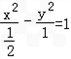 的左焦点F(-
的左焦点F(-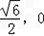 ),设M(x,y),
),设M(x,y),则|MF|2=(x+
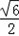 )2+y2,
)2+y2,由M点是右支上的一点,可知x≥
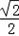 ,
,所以|MF|=
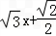 =2
=2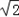 ,得x=
,得x=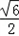 ,
,所以M(
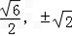 )。
)。(2)左顶点A(-
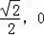 ),渐近线方程为:y=±
),渐近线方程为:y=±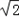 x
x过A与渐近线y=
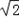 x平行的直线方程为y=
x平行的直线方程为y=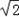 (x+
(x+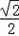 ),即y=
),即y=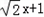 ,
,所以
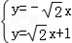 ,解得
,解得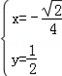
所以所求平行四边形的面积为S=
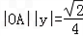 。
。(2)设直线PQ的方程为y=kx+b,因直线PQ与已知圆相切,故
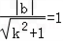 ,
,即b2=k2+1…①,
由
 ,得(2-k2)x2-2bkx-b2-1=0,
,得(2-k2)x2-2bkx-b2-1=0,设P(x1,y1),Q(x2,y2),则
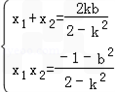 ,
,又y1y2=(kx1+b)(kx2+b)
所以
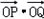 =x1x2+y1y2=(1+k2)x1x2+kb(x1+x2)+b2=
=x1x2+y1y2=(1+k2)x1x2+kb(x1+x2)+b2=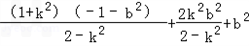 =
=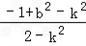
由①式可知
 ,故PO⊥OQ。
,故PO⊥OQ。
练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是