题目内容
已知函数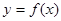 是定义域为
是定义域为 的奇函数,且当
的奇函数,且当 时,
时, ,(
,( 。
。
(1)求实数 的值;并求函数
的值;并求函数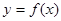 在定义域
在定义域 上的解析式;
上的解析式;
(2)求证:函数
 上是增函数。
上是增函数。
(1) ,
,
(2)利用定义法来作差变形定号下结论来得到证明。
解析试题分析:解:(1) 函数
函数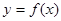 是定义域为
是定义域为 的奇函数,
的奇函数,
∴ ∴
∴ 2分
2分
当 时,
时,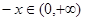 ,
, 4分
4分 5分
5分
(2)当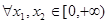 ,且
,且 ,
,
当 时,∵
时,∵ 为增函数,∴
为增函数,∴
又 也为增函数,
也为增函数, ,即
,即
当 时,∵
时,∵ 为减函数,∴
为减函数,∴
又 也为减函数,
也为减函数, ,即
,即
综上,都有 ,函数
,函数
 上是增函数。10分
上是增函数。10分
考点:函数的单调性
点评:主要是考查了函数的单调性的运用,属于中档题。

练习册系列答案
相关题目
 的定义域为
的定义域为  ,值域为
,值域为 ,则称函数
,则称函数 是
是 上的“四维方军”函数,求常数
上的“四维方军”函数,求常数 的值;
的值; 使函数
使函数 是区间
是区间 的值,否则,请说明理由.
的值,否则,请说明理由. 的奇函数
的奇函数 满足
满足 ,且当
,且当 时,
时,  .
. 上的解析式;
上的解析式; 取何值时,方程
取何值时,方程 在
在 上有解?
上有解?
 >
> 成立,则称函数
成立,则称函数 lnx是J函数时,求m的取值范围;
lnx是J函数时,求m的取值范围; g(1)的大小;
g(1)的大小; -2alnx(a>0)
-2alnx(a>0) .
. 在
在
 上单调性并证明你的结论;
上单调性并证明你的结论; 恒成立, 求整数
恒成立, 求整数 的最大值;
的最大值; .
. 是幂函数且在
是幂函数且在 上为减函数,函数
上为减函数,函数 在区间
在区间 上的最大值为2,试求实数
上的最大值为2,试求实数 的值。
的值。