题目内容
已知双曲线的中心在坐标原点,焦点在x轴上,实轴长为2.一条斜率为1的直线l过右焦点F与双曲线交于A,B两点,以AB为直径的圆与右准线交于M,N两点.
(1)若双曲线的离心率为2,求圆的半径;
(2)设AB的中点为H,若![]() ,求双曲线的方程.
,求双曲线的方程.
答案:
解析:
提示:
解析:
|
解答:(1)设所求方程为 由已知2a=2,∴a=1,又e= ∴双曲线方程为 设A(x1,y1),B(x2,y2),则 ∴ ∴r=3. (2)设双曲线方程为 ∴ 设半径为R, ∵ ∴ ∴ |
提示:
|
分析:(1)求圆的半径可用直线上的两点间的距离公式.(2) 说明:本题主要考查了圆锥曲线的有关性质,向量的定义及运算,分析问题的能力及数学计算能力. |

练习册系列答案
相关题目
 ,∴
,∴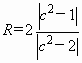 ,∴
,∴