题目内容

（2011•潍坊二模）已知双曲线的中心在坐标原点，焦点在x轴上，且一条渐近线为直线
3
x+y=0，则该双曲线的离心率等于
2
2
．
分析：先把直线方程整理成y=-
3
x，进而可知a和b的关系，利用c=
b2+a2
进而求得a和c的关系式，则双曲线的离心率可得．
解答：解：整理直线方程得y=-
3
x
∴
b
a
=
3
，即b=
3
a
∴c=
b2+a2
=2a
∴e=
c
a
=2
故答案为：2．
点评：本题主要考查了双曲线的简单性质．考查了学生对双曲线方程基础知识的掌握和运用．
练习册系列答案
相关题目
（2011•潍坊二模）设p：
xx-2
＜0，q：0＜x＜m，若p是q成立的充分不必要条件，则m的取值范围是
（2，+∞）
（2，+∞）
．
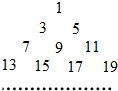（2011•潍坊二模）已知数列an=2n-1（n∈N*），把数列{an}的各项排成如图所示的三角形数阵，记（m，n）表示该数阵中第m行中从左到右的第n个数，则S（10，6）对应于数阵中的数是
101
101
．
（2011•潍坊二模）已知
m
=(cos?x，sin?x)，
n
=(cos?x，2
3
cos?x-sin?x)，?＞0，函数f(x)=
m
•
n
+|
m
|，x1，x2是集合M={x|f（x）=1}中任意两个元素，且|x1-x2|的最小值为
π
2
．
（1）求?的值．
（2）在△ABC中，a，b，c分别是A，B，C的对边．f(A)=2，c=2，S△ABC=
3
2
，求a的值．
（2011•潍坊二模）运行如图的程序框图，当输入m=-4时的输出结果为n，若变量x，y满足
x+y≤3
x-y≥-1
y≥n
，则目标函数z=2x+y的最大值为
5
5
．
（2011•潍坊二模）已知偶函数f（x）对?x∈R满足f（2+x）=f（2-x）且当-2≤x≤0时，f（x）=log2（1-x），则f（2011）的值为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网