题目内容
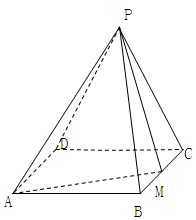
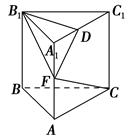
如图,在四棱锥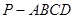 中,底面
中,底面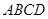 为矩形,
为矩形,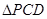 为等边三角形,
为等边三角形,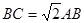 ,点
,点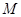 为
为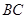 中点,平面
中点,平面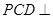 平面
平面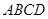 .
.
(1)求异面直线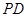 和
和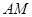 所成角的余弦值;
所成角的余弦值;
(2)求二面角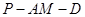 的大小.
的大小.
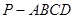 中,底面
中,底面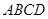 为矩形,
为矩形,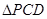 为等边三角形,
为等边三角形,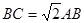 ,点
,点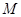 为
为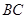 中点,平面
中点,平面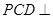 平面
平面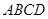 .
.
(1)求异面直线
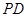 和
和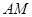 所成角的余弦值;
所成角的余弦值;(2)求二面角
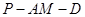 的大小.
的大小.(1)异面直线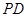 和
和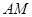 所成角的余弦值为
所成角的余弦值为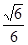 ;(2)二面角
;(2)二面角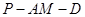 的大小为
的大小为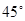 .
.
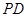 和
和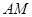 所成角的余弦值为
所成角的余弦值为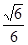 ;(2)二面角
;(2)二面角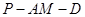 的大小为
的大小为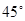 .
.试题分析:(1)建立如图所示坐标系,写出各点的空间坐标,利用
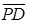 ,
,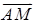 夹角的余弦,得出两异面直线
夹角的余弦,得出两异面直线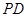 和
和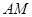 所成角的余弦值. (2)利用平面
所成角的余弦值. (2)利用平面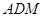 的法向量与平面
的法向量与平面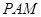 的法向量的夹角,求出二面角的大小.
的法向量的夹角,求出二面角的大小.试题解析:

解:取
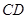 的中点
的中点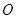 ,连接
,连接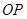 ,
,
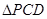 为等边三角形,
为等边三角形,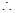
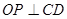 ,又平面
,又平面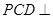 平面
平面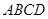 ,
,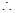
 2分
2分以
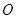 为原点,过点
为原点,过点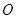 垂直
垂直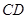 的直线为
的直线为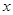 轴,
轴,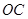 为
为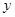 轴,
轴,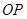 为
为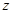 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系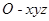 .
.
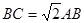 ,不妨设
,不妨设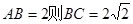 ,依题意可得:
,依题意可得: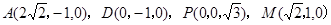 3分
3分(1)
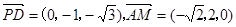 ,
,从而
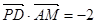 ,
,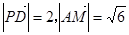
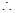
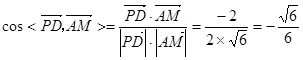 5分
5分于是异面直线
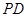 和
和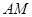 所成角的余弦值为
所成角的余弦值为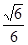 .6分
.6分(2)因为
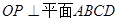 ,所以
,所以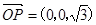 是平面
是平面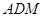 的法向量,8分
的法向量,8分设平面
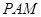 的法向量为
的法向量为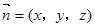 ,又
,又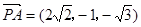 ,
,由
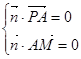 即
即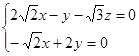 ,令
,令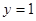 得
得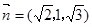 10分
10分于是
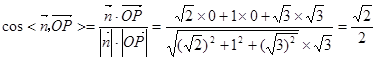 11分
11分从而二面角
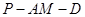 的大小为
的大小为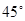 . 12分
. 12分
练习册系列答案
相关题目
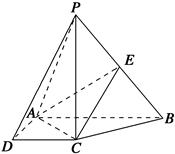
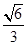 ,求直线PA与平面EAC所成角的正弦值.
,求直线PA与平面EAC所成角的正弦值.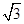 ,点D为AC的中点,点E在线段AA1上.
,点D为AC的中点,点E在线段AA1上.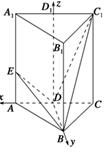
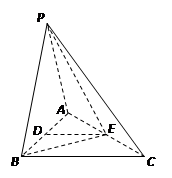
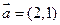 围绕原点按逆时针方向旋转
围绕原点按逆时针方向旋转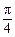 得到向量
得到向量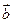 ,则向量
,则向量 ,
, ,
,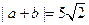 ,则
,则 ( )
( )
