题目内容
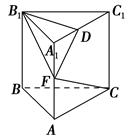
如图所示,在直三棱柱ABC-A1B1C1中,底面是∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF=________时,CF⊥平面B1DF.

a或2a
法一:由已知得B1D⊥平面AC1,
又CF?平面AC1,∴B1D⊥CF,
故若CF⊥平面B1DF,则必有CF⊥DF.
设AF=x(0<x<3a),则CF2=x2+4a2,
DF2=a2+(3a-x)2,又CD2=a2+9a2=10a2,
∴10a2=x2+4a2+a2+(3a-x)2,
解得x=a或2a.
法二:分别以BA、BC、BB1所在直线为x轴、y轴、z轴建立空间直角坐标系B-xyz,
则B(0,0,0),B1(0,0,3a),设F(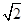 a,0,m),D
a,0,m),D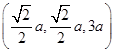 ,C(0,
,C(0,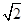 a,0),
a,0),
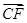 =(
=(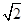 a,-
a,-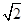 a,m),
a,m),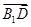 =
=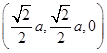 ,
,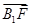 =(
=(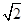 a,0,m-3a),
a,0,m-3a),
∵CF⊥面B1DF,∴CF⊥B1F,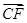 ⊥
⊥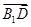 ,即
,即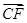 ·
·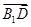 =0,
=0,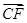 ·
·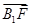 =0,
=0,
可得2a2+m(m-3a)=0,解得m=a或2a.
又CF?平面AC1,∴B1D⊥CF,
故若CF⊥平面B1DF,则必有CF⊥DF.
设AF=x(0<x<3a),则CF2=x2+4a2,
DF2=a2+(3a-x)2,又CD2=a2+9a2=10a2,
∴10a2=x2+4a2+a2+(3a-x)2,
解得x=a或2a.
法二:分别以BA、BC、BB1所在直线为x轴、y轴、z轴建立空间直角坐标系B-xyz,
则B(0,0,0),B1(0,0,3a),设F(
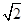 a,0,m),D
a,0,m),D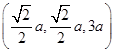 ,C(0,
,C(0,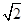 a,0),
a,0),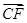 =(
=(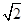 a,-
a,-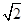 a,m),
a,m),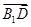 =
=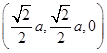 ,
,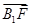 =(
=(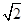 a,0,m-3a),
a,0,m-3a),∵CF⊥面B1DF,∴CF⊥B1F,
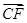 ⊥
⊥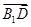 ,即
,即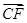 ·
·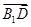 =0,
=0,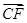 ·
·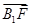 =0,
=0,可得2a2+m(m-3a)=0,解得m=a或2a.

练习册系列答案
相关题目
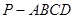 中,底面
中,底面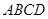 为矩形,
为矩形,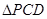 为等边三角形,
为等边三角形,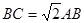 ,点
,点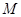 为
为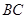 中点,平面
中点,平面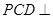 平面
平面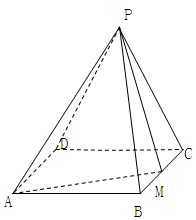
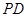 和
和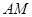 所成角的余弦值;
所成角的余弦值;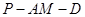 的大小.
的大小.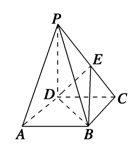
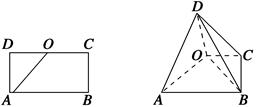
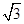 .
.
 中,
中,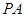 ⊥平面
⊥平面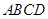 ,底面
,底面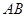 ∥
∥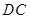 ,
,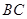 ,
,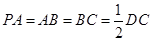 ,点
,点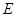 在棱
在棱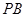 上,且
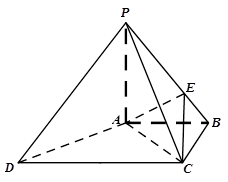
上,且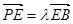 .
.
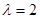 时,求证:
时,求证: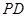 ∥面
∥面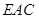 ;
;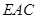 所成角为
所成角为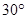 ,求实数
,求实数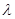 的值.
的值.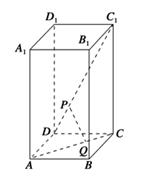
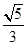
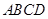 中,
中,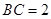 ,
,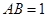 ,
,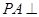 平面
平面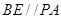 ,
,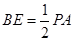 ,
,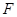 为
为 的中点.
的中点.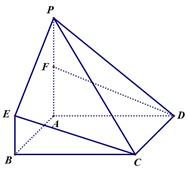
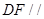 平面
平面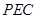 .
.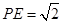 ,求平面
,求平面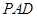 所成锐二面角的余弦值.
所成锐二面角的余弦值.