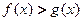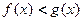题目内容
已知二次函数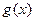 的图像经过坐标原点,且满足
的图像经过坐标原点,且满足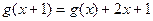 ,设函数
,设函数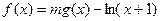 ,其中
,其中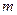 为非零常数
为非零常数
(I)求函数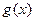 的解析式;
的解析式;
(II)当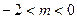 时,判断函数
时,判断函数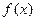 的单调性并且说明理由;
的单调性并且说明理由;
(III)证明:对任意的正整数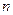 ,不等式
,不等式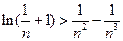 恒成立
恒成立
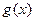 的图像经过坐标原点,且满足
的图像经过坐标原点,且满足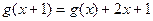 ,设函数
,设函数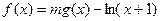 ,其中
,其中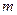 为非零常数
为非零常数(I)求函数
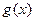 的解析式;
的解析式;(II)当
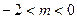 时,判断函数
时,判断函数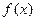 的单调性并且说明理由;
的单调性并且说明理由;(III)证明:对任意的正整数
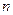 ,不等式
,不等式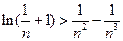 恒成立
恒成立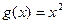
(Ⅰ)设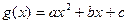 ,
,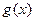 的图象经过坐标原点,所以c=0.
的图象经过坐标原点,所以c=0.
∵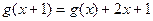 ∴
∴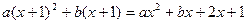
即: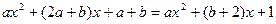
∴a=1,b=0,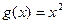 ;……………………………………4分
;……………………………………4分
(Ⅱ)函数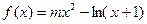 的定义域为
的定义域为
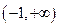 .
.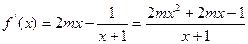 ,
,
令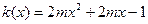 ,
,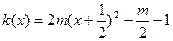 ,
,
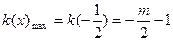 ,
,
∵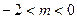 ,∴
,∴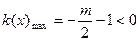 ,
,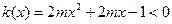 在
在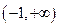 上恒成立,
上恒成立,
即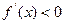 ,当
,当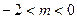 时,函数
时,函数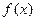 在定义域
在定义域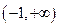 上单调递减.………9分
上单调递减.………9分
(III)当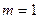 时,
时,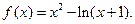 ,令
,令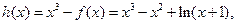
则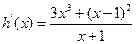 在
在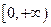 上恒正,
上恒正,
∴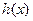 在
在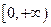 上单调递增,当
上单调递增,当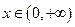 时,恒有
时,恒有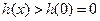 .,
.,
即当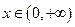 时,有
时,有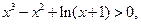
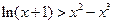 ,
,
对任意正整数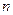 ,取
,取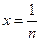 得
得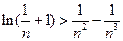 .………………13分
.………………13分
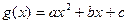 ,
,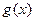 的图象经过坐标原点,所以c=0.
的图象经过坐标原点,所以c=0.∵
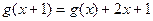 ∴
∴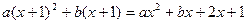
即:
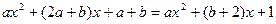
∴a=1,b=0,
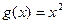 ;……………………………………4分
;……………………………………4分(Ⅱ)函数
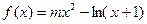 的定义域为
的定义域为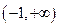 .
.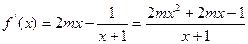 ,
,令
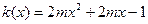 ,
,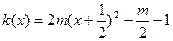 ,
,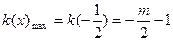 ,
,∵
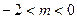 ,∴
,∴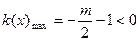 ,
,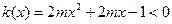 在
在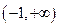 上恒成立,
上恒成立,即
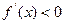 ,当
,当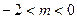 时,函数
时,函数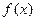 在定义域
在定义域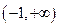 上单调递减.………9分
上单调递减.………9分(III)当
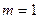 时,
时,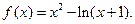 ,令
,令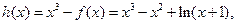
则
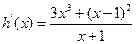 在
在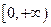 上恒正,
上恒正,∴
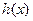 在
在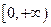 上单调递增,当
上单调递增,当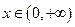 时,恒有
时,恒有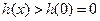 .,
.,即当
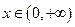 时,有
时,有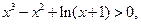
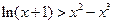 ,
,对任意正整数
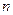 ,取
,取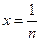 得
得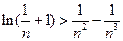 .………………13分
.………………13分
练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
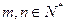 且
且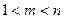 ,试用导数证明不等式:
,试用导数证明不等式: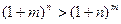 .
.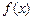 的定义域为
的定义域为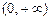 ,
,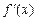 ,且对任意正数
,且对任意正数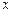 均有
均有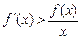 ,
,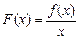 在
在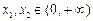 ,比较
,比较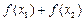 与
与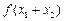 的大小,并证明你的结论;
的大小,并证明你的结论;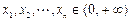 ,若
,若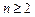 ,比较
,比较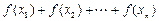 与
与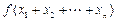 的大小,并证明你的结论.
的大小,并证明你的结论.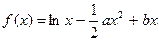
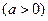 且
且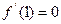 .
.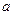 式子表示
式子表示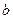 ;(Ⅱ)求
;(Ⅱ)求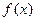 的单调区间;(Ⅲ)若
的单调区间;(Ⅲ)若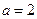 ,试求
,试求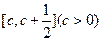 上的最大值.
上的最大值.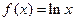 ,
,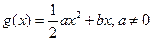 。
。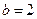 ,且函数
,且函数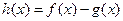 存在单调递减区间,求
存在单调递减区间,求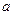 的取值范围;
的取值范围;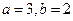 时,求函数
时,求函数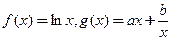 ,它们的图象在
,它们的图象在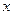 轴上的公共点处有公切线,则当
轴上的公共点处有公切线,则当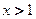 时,
时,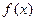 与
与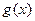 的大小关系是 ( )
的大小关系是 ( )