题目内容
已知函数 的图象经过
的图象经过
 其中
其中 为自然对数的底数,
为自然对数的底数,
 .
.
(Ⅰ)求实数 ;
;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)证明:对于任意的 ,都有
,都有 成立.
成立.
 的图象经过
的图象经过
 其中
其中 为自然对数的底数,
为自然对数的底数,
 .
.(Ⅰ)求实数
 ;
;(Ⅱ)求
 的单调区间;
的单调区间;(Ⅲ)证明:对于任意的
 ,都有
,都有 成立.
成立.(Ⅰ)由 的图象过点
的图象过点 得
得
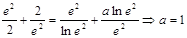 .
.
(Ⅱ)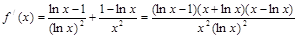
由 知
知 ,令
,令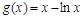
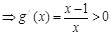 ,故
,故 在
在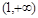 上为增函数,当
上为增函数,当 时,
时,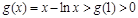
令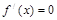 得
得 ,令
,令 得,
得, ,令
,令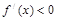 得
得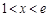
故 的增区间为
的增区间为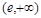 ,减区间为
,减区间为 .
.
(Ⅲ)由(2)知, 在区间
在区间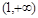 上的最小值为
上的最小值为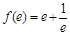
即当 时,
时,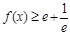 恒成立
恒成立
当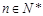 时,令
时,令 ,则有
,则有
即
故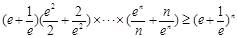 成立.
成立.
 的图象过点
的图象过点 得
得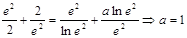 .
. (Ⅱ)
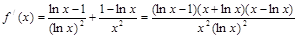
由
 知
知 ,令
,令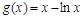
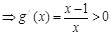 ,故
,故 在
在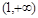 上为增函数,当
上为增函数,当 时,
时,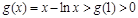
令
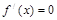 得
得 ,令
,令 得,
得, ,令
,令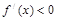 得
得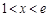
故
 的增区间为
的增区间为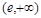 ,减区间为
,减区间为 .
. (Ⅲ)由(2)知,
 在区间
在区间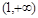 上的最小值为
上的最小值为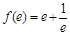
即当
 时,
时,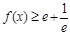 恒成立
恒成立当
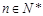 时,令
时,令 ,则有
,则有
即

故
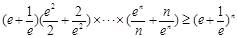 成立.
成立. 略

练习册系列答案
相关题目
 上的点到直线
上的点到直线 的最短距离是_____________
的最短距离是_____________ 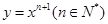 在点(1,1)处的切线与
在点(1,1)处的切线与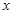 轴的交点的横坐标为
轴的交点的横坐标为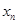 ,令
,令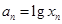 ,则
,则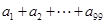 的值为 .
的值为 .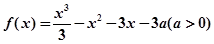 (12分)
(12分)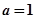 ,点P为曲线
,点P为曲线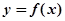 上一个动点,求以P为切点的切线斜率取得最小值时的切线方程;
上一个动点,求以P为切点的切线斜率取得最小值时的切线方程;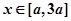 时,
时,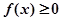 恒成立,求
恒成立,求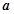 的取值范围。
的取值范围。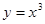 在点
在点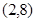 处的切线方程为( ).
处的切线方程为( ).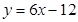
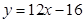
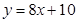
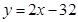
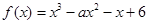 在
在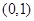 内单调递减,则实数
内单调递减,则实数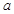 的取值范围是( )
的取值范围是( )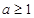



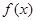 的导数为
的导数为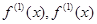 的导数为
的导数为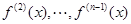 的导数为
的导数为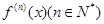 。若
。若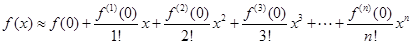
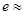 (用分数表示)
(用分数表示) 若
若 ,则
,则 的值为( )
的值为( )



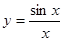 的导数为________.
的导数为________.