题目内容
【题目】某旅游为了解2015年国庆节期间参加某境外旅游线路的游客的人均购物消费情况,随机对50人做了问卷调查,得如下频数分布表:
人均购物消费情况 | [0,2000] | (2000,4000] | (4000,6000] | (6000,8000] | (8000,10000] |
额数 | 15 | 20 | 9 | 3 | 3 |
附:临界值表参考公式:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
(1)做出这些数据的频率分布直方图并估计次境外旅游线路游客的人均购物的消费平均值;
(2)在调查问卷中有一项是“您会资助失学儿童的金额?”,调查情况如表,请补全如表,并说明是否有95%以上的把握认为资助数额多于或少于500元和自身购物是否到4000元有关?
人均购物消费不超过4000元 | 人均购物消费超过4000元 | 合计 | |
资助超过500元 | 30 | ||
资助不超过500元 | 6 | ||
合计 |
【答案】
(1)解:作出频率分布直方图如图所示:
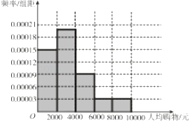
人均购物消费平均值 ![]() =(1000×0.00015+3000×0.0002+5000×0.00009+7000×0.00003+9000×0.00003)×2000=3360.
=(1000×0.00015+3000×0.0002+5000×0.00009+7000×0.00003+9000×0.00003)×2000=3360.
(2)解:2×2列联表如下:
人均购物消费 不超过4000元 | 人均购物消费 超过4000元 | 合计 | |
资助超过500元 | 30 | 9 | 39 |
资助不超过500元 | 5 | 6 | 11 |
合计 | 35 | 15 | 50 |
K2= ![]() =4.046>3.841.
=4.046>3.841.
∴由95%的把握认为资助数额多余或少于500元与自身购物是否到4000元有关
【解析】(1)根据消费情况计算各组的频率及频率分布直方图的高度作图;(2)列联表计算K2 , 根据附表进行判断.

 阅读快车系列答案
阅读快车系列答案【题目】已知下表为函数![]() 部分自変量取值及其对应函数值,为了便于研究,相关函数值取非整数值时,取值精确到0.01.
部分自変量取值及其对应函数值,为了便于研究,相关函数值取非整数值时,取值精确到0.01.
| 0.61 | -0.59 | -0.56 | -0.35 | 0 | 0.26 | 0.42 | 1.57 | 3.27 |
| 0.07 | 0.02 | -0.03 | -0.22 | 0 | 0.21 | 0.20 | -10.04 | -101.63 |
据表中数据,研究该函数的一些性质;
(1)判断函数![]() 的奇偶性,并证明;
的奇偶性,并证明;
(2)判断函数![]() 在区间[0.55,0.6]上是否存在零点,并说明理由;
在区间[0.55,0.6]上是否存在零点,并说明理由;
(3)判断![]() 的正负,并证明函数
的正负,并证明函数![]() 在
在![]() 上是单调递减函数.
上是单调递减函数.
【题目】某校有150名学生参加了中学生环保知识竞赛,为了解成绩情况,现从中随机抽取50名学生的成绩进行统计(所有学生成绩均不低于60分).请你根据尚未完成的频率分布表,解答下列问题:
(1)写出M 、N 、p、q(直接写出结果即可),并作出频率分布直方图;
(2)若成绩在90分以上学生获得一等奖,试估计全校所有参赛学生获一等奖的人数;
(3)现从所有一等奖的学生中随机选择2名学生接受采访,已知一等奖获得者中只有2名女生,求恰有1名女生接受采访的概率.
分组 | 频数 | 频率 | |
第1组 | [60,70) | M | 0.26 |
第2组 | [70,80) | 15 | p |
第3组 | [80,90) | 20 | 0.40 |
第4组 | [90,100] | N | q |
合计 | 50 | 1 | |


