题目内容
【题目】用数学归纳法证明:(n+1)+(n+2)+…+(n+n)= ![]() (n∈N*)
(n∈N*)
【答案】证明:①n=1时,左边=2,右边=2,等式成立; ②假设n=k时,结论成立,即:(k+1)+(k+2)+…+(k+k)= ![]()
则n=k+1时,等式左边=(k+2)+(k+3)+…+(k+k+1)+(k+1+k+1)= ![]() +3k+2=
+3k+2= ![]()
故n=k+1时,等式成立
由①②可知:(n+1)+(n+2)+…+(n+n)= ![]() (n∈N*)成立
(n∈N*)成立
【解析】根据数学归纳法的证题步骤,先证n=1时,等式成立;再假设n=k时,等式成立,再证n=k+1时等式成立.关键是注意n=k+1时等式左边与n=k时的等式左边的差,即为n=k+1时等式左边增加的项
【考点精析】关于本题考查的数学归纳法的定义,需要了解数学归纳法是证明关于正整数n的命题的一种方法才能得出正确答案.

练习册系列答案
相关题目
【题目】(本小题满分12分)
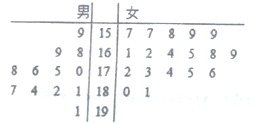
某学校用简单随机抽样方法抽取了100名同学,对其日均课外阅读时间(单位:分钟)进行调查,结果如下:
t |
|
|
|
|
|
|
男同学人数 | 7 | 11 | 15 | 12 | 2 | 1 |
女同学人数 | 8 | 9 | 17 | 13 | 3 | 2 |
若将日均课外阅读时间不低于60分钟的学生称为“读书迷”.
(1)将频率视为概率,估计该校4000名学生中“读书迷”有多少人?
(2)从已抽取的8名“读书迷”中随机抽取4位同学参加读书日宣传活动.
(i)求抽取的4位同学中既有男同学又有女同学的概率;
(ii)记抽取的“读书迷”中男生人数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望