Question

在平面直角坐标系xOy中，已知射线 OA：x-y=0（x≥0），OB：x+2y=0（x≥0），过点P（2，0）作直线分别交射线OA、OB于点E、F，若

EP

=

PF

，则直线EF的斜率为

-2

．

Answer 1

分析：由题意设E（a，a），B（-2b，b），则

EP

=(2-a，-a)，

PF

=(-2b-2，b)，由

EP

=

PF

，解得a=

4

3

，b=-

4

3

，由此能求出直线EF的斜率．

解答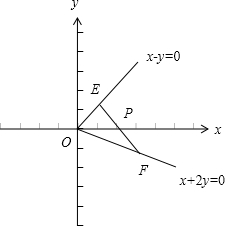：解：∵射线 OA：x-y=0（x≥0），OB：x+2y=0（x≥0），过点P（2，0）作直线分别交射线OA、OB于点E、F，
∴如图，设E（a，a），B（-2b，b），
则

EP

=(2-a，-a)，

PF

=(-2b-2，b)，
∵

EP

=

PF

，
∴

2-a=-2b-2 -a=b

，
∴a=

4

3

，b=-

4

3

，
∴E（

4

3

，

4

3

），
∴直线EF的斜率k=

4 3 -0

4 3 -2

=-2．
故答案为：-2．

点评：本题考查直线的斜率的求法，是基础题．解题时要认真审题，仔细解答．