题目内容
【题目】已知双曲线![]() 的左右焦点为
的左右焦点为![]() 为它的中心,
为它的中心,![]() 为双曲线右支上的一点,
为双曲线右支上的一点,![]() 的内切圆圆心为
的内切圆圆心为![]() ,且圆
,且圆![]() 与
与![]() 轴相切于
轴相切于![]() 点,过
点,过![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,若双曲线的离心率为
,若双曲线的离心率为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 与
与![]() 关系不确定
关系不确定
【答案】A
【解析】
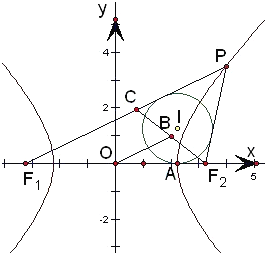
F1(﹣c,0)、F2(c,0),内切圆与x轴的切点是点A
∵|PF1|﹣|PF2|=2a,及圆的切线长定理知,
|AF1|﹣|AF2|=2a,设内切圆的圆心横坐标为x,
则|(x+c)﹣(c﹣x)|=2a
∴x=a;
|OA|=a,
在△PCF2中,由题意得,F2B⊥PI于B,延长交F1F2于点C,利用△PCB≌△PF2B,可知PC=PF2,
∴在三角形F1CF2中,有:
OB=![]() CF1=
CF1=![]() (PF1﹣PC)=
(PF1﹣PC)=![]() (PF1﹣PF2)=
(PF1﹣PF2)=![]() ×2a=a.
×2a=a.
∴|OB|=|OA|.
故选:A.

练习册系列答案
相关题目
【题目】据报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改革”引起广泛关注,为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人进行调查,就“是否取消英语听力”问题进行了问卷调查统计,结果如下表:
态度 调查人群 | 应该取消 | 应该保留 | 无所谓 |
在校学生 | 2100人 | 120人 |
|
社会人士 | 600人 |
|
|
(1)已知在全体样本中随机抽取![]() 人,抽到持“应该保留”态度的人的概率为
人,抽到持“应该保留”态度的人的概率为![]() ,现用分层抽样的方法在所有参与调查的人中抽取
,现用分层抽样的方法在所有参与调查的人中抽取![]() 人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取![]() 人,再平均分成两组进行深入交流,求第一组中在校学生人数
人,再平均分成两组进行深入交流,求第一组中在校学生人数![]() 的分布列和数学期望.
的分布列和数学期望.