题目内容
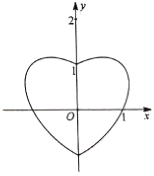
【题目】已知曲线![]() ,把
,把![]() 上各点横坐标伸长为原来的2倍,纵坐标不变,得到函数
上各点横坐标伸长为原来的2倍,纵坐标不变,得到函数![]() 的图象,关于
的图象,关于![]() 有下述四个结论:
有下述四个结论:
(1)函数![]() 在
在![]() 上是减函数;
上是减函数;
(2)方程![]() 在
在![]() 内有2个根;
内有2个根;
(3)函数![]() (其中
(其中![]() )的最小值为
)的最小值为![]() ;
;
(4)当![]() ,且
,且![]() 时,
时,![]() ,则
,则![]() .
.
其中正确结论的个数为( )
A.1B.2C.3D.4
【答案】C
【解析】
由三角函数图象平移法则得出函数![]() 的解析式,再对题目中的命题分析、判断真假性即可.
的解析式,再对题目中的命题分析、判断真假性即可.
解:曲线![]() ,把
,把![]() 上各点横坐标伸长为原来的2倍,纵坐标不变,
上各点横坐标伸长为原来的2倍,纵坐标不变,
得![]() 的图象,所以函数
的图象,所以函数![]() ;
;
对于(1),当![]() ,
,![]() ,
,![]() ,
,![]() 上是减函数,所以(1)正确;
上是减函数,所以(1)正确;
对于(2),方程![]() ,得
,得![]() ,
,![]() ,
,![]() ;
;
![]() 时,两函数图象没有交点,所以原方程没有实数根,所以(2)错误;
时,两函数图象没有交点,所以原方程没有实数根,所以(2)错误;
对于(3),函数![]() ,
,
则![]() ,
,
令![]() ,解得
,解得![]() 或
或![]() ,
,![]() 时
时![]() 取得最小值为
取得最小值为![]() ,所以(3)正确;
,所以(3)正确;
对于(4),![]() ,
,![]() ,
,![]() ;
;
当![]() ,
,![]() ,
,![]() ,且
,且![]() 时,
时,![]() ,
,
则![]() ,所以(4)正确.
,所以(4)正确.
综上知,其中正确结论的序号是(1)、(3)、(4),共3个.
故选:C.

练习册系列答案
相关题目
【题目】某企业为确定下一年投入某种产品的研发费用,需了解年研发费用![]() (单位:千万元)对年销售量
(单位:千万元)对年销售量![]() (单位:千万件)的影响,统计了近
(单位:千万件)的影响,统计了近![]() 年投入的年研发费用
年投入的年研发费用![]() 与年销售量
与年销售量![]() 的数据,得到散点图如图所示.
的数据,得到散点图如图所示.
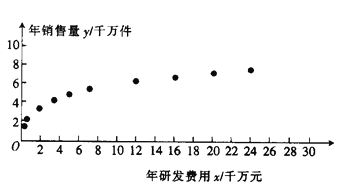
(1)利用散点图判断![]() 和
和![]() (其中
(其中![]() 均为大于
均为大于![]() 的常数)哪一个更适合作为年销售量
的常数)哪一个更适合作为年销售量![]() 和年研发费用
和年研发费用![]() 的回归方程类型(只要给出判断即可,不必说明理由)
的回归方程类型(只要给出判断即可,不必说明理由)
(2)对数据作出如下处理,令![]() ,得到相关统计量的值如下表:根据第(1)问的判断结果及表中数据,求
,得到相关统计量的值如下表:根据第(1)问的判断结果及表中数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
|
|
|
|
15 | 15 | 28.25 | 56.5 |
(3)已知企业年利润![]() (单位:千万元)与
(单位:千万元)与的关系为
![]() (其中
(其中![]() ),根据第(2)问的结果判断,要使得该企业下一年的年利润最大,预计下一年应投入多少研发费用?
),根据第(2)问的结果判断,要使得该企业下一年的年利润最大,预计下一年应投入多少研发费用?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为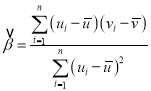 ,
,![]()