题目内容
 已知椭圆
已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| F1Q |
| PT |
| TF2 |
| TF2 |
(Ⅰ)设x为点P的横坐标,证明|
| F1P |
| c |
| a |
(Ⅱ)求点T的轨迹C的方程;
(Ⅲ)试问:在点T的轨迹C上,是否存在点M,使△F1MF2的面积S=b2.若存在,求∠F1MF2的正切值;若不存在,请说明理由.
| 分析:(Ⅰ)证法一:设点P的坐标为(x,y), 由题设条件知|
由此能够推导出|
证法二:设点P的坐标为(x,y).记|
由r1+r2=2a,r12+r22=4cx,能够推导出|
证法三:设点P的坐标为(x,y).椭圆的左准线方程为a+
由椭圆第二定义得
(Ⅱ)解法一:设点T的坐标为(x,y).当|
当|
在△QF1F2中,|
解法二:在推导出T为线段F2Q的中点的基础上,设点Q的坐标为(x',y'), 由中点坐标公式和|
(Ⅲ)解法一:C上存在点M(x0,y0)使S=b2的充要条件是
由③得|y0|≤a,由④得|y0|≤
解法二:C上存在点M(x0,y0)使S=b2的充要条件是
由④得|y0|≤
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
解答: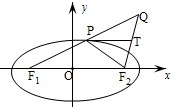 (Ⅰ)证法一:设点P的坐标为(x,y). (Ⅰ)证法一:设点P的坐标为(x,y).由P(x,y)在椭圆上,得|
由x≥a,知a+
证法二:设点P的坐标为(x,y).记|
则r1=
由r1+r2=2a,r12+r22=4cx,得|
证法三:设点P的坐标为(x,y).椭圆的左准线方程为a+
由椭圆第二定义得
由x≥-a,知a+
(Ⅱ)解法一:设点T的坐标为(x,y). 当|
当|
又|
在△QF1F2中,|
综上所述,点T的轨迹C的方程是x2+y2=a2. 解法二:设点T的坐标为(x,y).当|
当|
又,|
设点Q的坐标为(x',y'),则
因此
由|
将①代入②,可得x2+y2=a2. 综上所述,点T的轨迹C的方程是x2+y2=a2. (Ⅲ)解法一:C上存在点M(x0,y0)使S=b2的充要条件是
由③得|y0|≤a,由④得|y0|≤
当a<
当a≥
由
S=
解法二:C上存在点M(x0,y0)使S=b2的充要条件是
由④得|y0|≤ 
练习册系列答案
 世纪百通期末金卷系列答案 世纪百通期末金卷系列答案
相关题目
|