题目内容
 (2012•青岛一模)如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=
(2012•青岛一模)如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=| 2 |
(Ⅰ) 证明:OE∥平面ABC1;
(Ⅱ)证明:A1C⊥平面BDE.
分析:(Ⅰ) 证明OE∥AC1,然后利用直线与平面平行的判定定理证明OE∥平面ABC1;
(Ⅱ)连接A1C1,证明A1C⊥AC1,A1C⊥OE,证明BD⊥平面A1C,然后证明A1C⊥平面BDE.
(Ⅱ)连接A1C1,证明A1C⊥AC1,A1C⊥OE,证明BD⊥平面A1C,然后证明A1C⊥平面BDE.
解答:解:(1)证明:因为EC1=EC,AO=OC.所以OE∥AC1.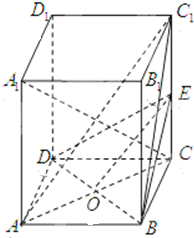
因为AC1?平面ABC1,OE?平面ABC1,所以OE∥平面ABC1;
(Ⅱ)连接A1C1,因为AB=a所以A1C1=
a.
所以四边形ACC1A1为正方形,所以A1C⊥AC1,
因为OE∥AC1.
所以A1C⊥OE,
又因为BD⊥AC,BD⊥AA1,AC∩AA1=A
所以BD⊥平面AA1C,所以BD⊥A1C,
又因为OE∩BD=O,所以A1C⊥平面BDE.

因为AC1?平面ABC1,OE?平面ABC1,所以OE∥平面ABC1;
(Ⅱ)连接A1C1,因为AB=a所以A1C1=
| 2 |
所以四边形ACC1A1为正方形,所以A1C⊥AC1,
因为OE∥AC1.
所以A1C⊥OE,
又因为BD⊥AC,BD⊥AA1,AC∩AA1=A
所以BD⊥平面AA1C,所以BD⊥A1C,
又因为OE∩BD=O,所以A1C⊥平面BDE.
点评:本题考查直线与平面平行,直线与平面垂直,考查判定定理的应用,考查空间想象能力,逻辑推理能力.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
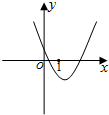 (2012•青岛一模)已知a>b,函数f(x)=(x-a)(x-b)的图象如图所示,则函数g(x)=loga(x+b)的图象可能为
(2012•青岛一模)已知a>b,函数f(x)=(x-a)(x-b)的图象如图所示,则函数g(x)=loga(x+b)的图象可能为