题目内容
(2012•青岛一模)已知等差数列{an}的公差大于零,且a2,a4是方程x2-18x+65=0的两个根;各项均为正数的等比数列{bn}的前n项和为Sn,且满足b3=a3,S3=13.
(1)求数列{an}、{bn}的通项公式;
(2)若数列{cn}满足cn=
,求数列{cn}的前n项和Tn.
(1)求数列{an}、{bn}的通项公式;
(2)若数列{cn}满足cn=
|
分析:(1)设{an}的公差为d,{bn}的公比为q,由题意及a2<a4,可求a2,a4,利用等差数列的通项公式可求a1,d,可求an,然后由等比数列的通项公式及求和可求b1,q,可求
(2)当n≤5时,Tn=a1+a2+…+an,利用等差数列的求和公式可求,当n>5时,Tn=T5+(b6+b7+…+bn),利用分组求和及等差、等比数列的求和公式可求
(2)当n≤5时,Tn=a1+a2+…+an,利用等差数列的求和公式可求,当n>5时,Tn=T5+(b6+b7+…+bn),利用分组求和及等差、等比数列的求和公式可求
解答:解:(1)设{an}的公差为d,{bn}的公比为q,则
由x2-18x+65=0解得x=5或x=13
因为d>0,所以a2<a4,则a2=5,a4=13
则
,解得a1=1,d=4
所以an=1+4(n-1)=4n-3…(4分)
因为
,因为q>0,解得b1=1,q=3
所以bn=3n-1…(7分)
(2)当n≤5时,Tn=a1+a2+…+an
=n+
×4=2n2-n…(9分)
当n>5时,Tn=T5+(b6+b7+…+bn)
=(2×52-5)+
=
所以Tn=
…(14分)
由x2-18x+65=0解得x=5或x=13
因为d>0,所以a2<a4,则a2=5,a4=13
则
|
所以an=1+4(n-1)=4n-3…(4分)
因为
|
所以bn=3n-1…(7分)
(2)当n≤5时,Tn=a1+a2+…+an
=n+
| n(n-1) |
| 2 |
当n>5时,Tn=T5+(b6+b7+…+bn)
=(2×52-5)+
| 33(1-3n-5) |
| 1-3 |
=
| 3n-153 |
| 2 |
所以Tn=
|
点评:本小题主要考查等差数列、等比数列的定义.运用基本量的思想求出数列的通项公式.考查分段函数、数列的求和的基本方法.运算求解能力,考查化归与转化思想.

练习册系列答案
相关题目
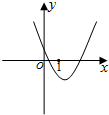 (2012•青岛一模)已知a>b,函数f(x)=(x-a)(x-b)的图象如图所示,则函数g(x)=loga(x+b)的图象可能为
(2012•青岛一模)已知a>b,函数f(x)=(x-a)(x-b)的图象如图所示,则函数g(x)=loga(x+b)的图象可能为