题目内容
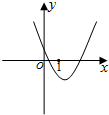（2012•青岛一模）已知a＞b，函数f（x）=（x-a）（x-b）的图象如图所示，则函数g（x）=loga（x+b）的图象可能为（ ）
分析：由a＞b，函数f（x）=（x-a）（x-b）的图象可知，a＞1＞b＞0．于是g（x）=loga（x+b）的图象是单调递增的，g（1）＞0，从而可得答案．
解答：解：由f（x）=（x-a）（x-b）的图象与a＞b得：a＞1＞b＞0．
∴g（x）=loga（x+b）的图象是单调递增的，可排除A，D，
又g（1）=loga（1+b）＞loga1=0，可排除C，
故选B．
∴g（x）=loga（x+b）的图象是单调递增的，可排除A，D，
又g（1）=loga（1+b）＞loga1=0，可排除C，
故选B．
点评：本题考查对数函数的图象与性质，由由a＞b与函数f（x）=（x-a）（x-b）的图象得到a＞1＞b＞0是关键，属于基础题．
练习册系列答案
相关题目