题目内容
(12分)已知函数f(x)=sinωx(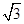 cosωx+sinωx)+
cosωx+sinωx)+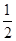 (ω∈R,x∈R)最小正周期为π,且图象关于直线x=
(ω∈R,x∈R)最小正周期为π,且图象关于直线x=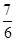 π对称.
π对称.
(1)求f(x)的最大值及对应的x的集合;
(2)若直线y=a与函数y=1-f(x),x∈[0,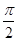 ]的图象有且只有一个公共点,求实数a的范围.
]的图象有且只有一个公共点,求实数a的范围.
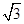 cosωx+sinωx)+
cosωx+sinωx)+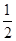 (ω∈R,x∈R)最小正周期为π,且图象关于直线x=
(ω∈R,x∈R)最小正周期为π,且图象关于直线x=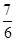 π对称.
π对称.(1)求f(x)的最大值及对应的x的集合;
(2)若直线y=a与函数y=1-f(x),x∈[0,
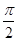 ]的图象有且只有一个公共点,求实数a的范围.
]的图象有且只有一个公共点,求实数a的范围. (1)最大值为2.此时x=k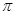 -
-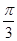 ,k
,k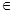 Z;(2)
Z;(2) 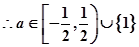
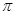 -
-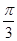 ,k
,k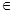 Z;(2)
Z;(2) 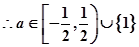
本试题主要是考查了三角函数的图像与性质,以及三角恒等变换的综合运用。求解函数图像与图像的交点问题。
(1)先将三角函数化简为单一三角函数,利用对称轴的性质,求解最值
(2)由于三角函数图像与直线y=a有且只有一个公点,则结合图像法得到参数a的取值范围。
解:(1)f(x)=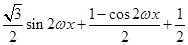
=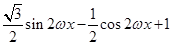 …………………………2分
…………………………2分
=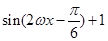 T=
T=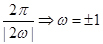 ………………3分
………………3分
若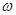 ="1" ,
="1" ,  此时
此时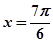 不是对称轴………4分
不是对称轴………4分
若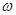 ="-1" ,
="-1" ,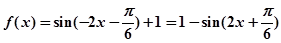 此时
此时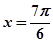 是对称轴…5分
是对称轴…5分
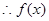 最大值为2.此时2x+
最大值为2.此时2x+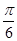 =2k
=2k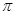 -
-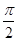
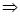 x=k
x=k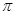 -
-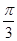 ,k
,k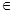 Z……………………6分
Z……………………6分
(2)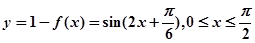 ,的图象与直线y=a的图象有且只有一个公点
,的图象与直线y=a的图象有且只有一个公点
 …………9分
…………9分
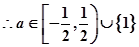 ……………………12分
……………………12分
(1)先将三角函数化简为单一三角函数,利用对称轴的性质,求解最值
(2)由于三角函数图像与直线y=a有且只有一个公点,则结合图像法得到参数a的取值范围。
解:(1)f(x)=
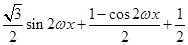
=
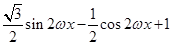 …………………………2分
…………………………2分=
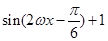 T=
T=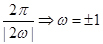 ………………3分
………………3分若
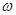 ="1" ,
="1" ,  此时
此时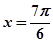 不是对称轴………4分
不是对称轴………4分若
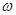 ="-1" ,
="-1" ,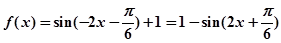 此时
此时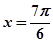 是对称轴…5分
是对称轴…5分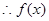 最大值为2.此时2x+
最大值为2.此时2x+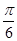 =2k
=2k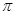 -
-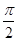
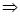 x=k
x=k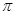 -
-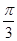 ,k
,k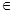 Z……………………6分
Z……………………6分(2)
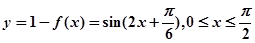 ,的图象与直线y=a的图象有且只有一个公点
,的图象与直线y=a的图象有且只有一个公点 …………9分
…………9分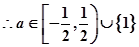 ……………………12分
……………………12分
练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
 的图象与
的图象与 轴交点的纵坐标为1,在相邻的两点
轴交点的纵坐标为1,在相邻的两点 ,
, 上
上 分别取得最大值和最小值.
分别取得最大值和最小值. 的最大和最小值分别为6和2,求
的最大和最小值分别为6和2,求 的值.
的值.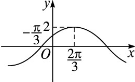
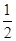 ,φ=-
,φ=-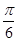
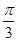
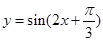 的图象向右平移
的图象向右平移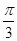 个单位,得到函数
个单位,得到函数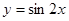 的图象;
的图象;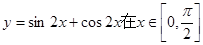 上的单调递增区间是
上的单调递增区间是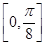 ;
;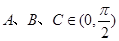 且
且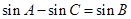 ,
,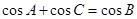 ,则
,则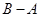 等于
等于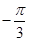 ;
;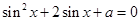 有解,则
有解,则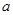 的取值范围是
的取值范围是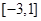 .
.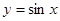 与函数
与函数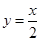 的图象有三个交点;
的图象有三个交点; 中,
中, 的对边分别为
的对边分别为 且
且 成等差数列.
成等差数列. 的范围.
的范围.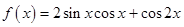 (
( R).
R). 的最小正周期和最大值;
的最小正周期和最大值;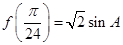 ,其中
,其中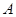 是面积为
是面积为 的锐角
的锐角 的内角,且
的内角,且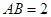 ,求边
,求边 和
和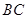 的长.
的长.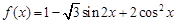 .
.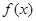 的最大值及取得最大值时的
的最大值及取得最大值时的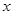 集合;
集合;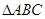 的角
的角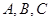 的对边分别为
的对边分别为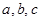 ,且
,且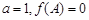 .求
.求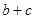 的取值范围
的取值范围 在
在 上有两个不等的实数根
上有两个不等的实数根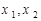 ,则
,则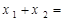 ( )
( )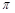
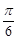
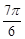
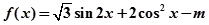 。
。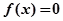 在
在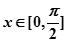 上有解,求
上有解,求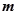 的取值范围;
的取值范围;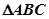 中,
中,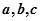 分别是
分别是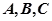 所对的边,当(1)中的
所对的边,当(1)中的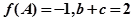 时,求
时,求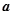 的最小值。
的最小值。