题目内容
若点A(m,0)到双曲线
-y2=1的实轴的一个端点的距离是A到双曲线上的各个点的距离的最小值,则m的取值范围是( )
| x2 |
| 4 |
| A.[-2,2] | B.[-
| ||||||||
C.[-
| D.(-∞,-
|
由题意知双曲线
-y2=1焦点在x轴上,且a=2,b=1,c=
,
∴双曲线的左、右顶点分别为为M(-2,0)、N(2,0);
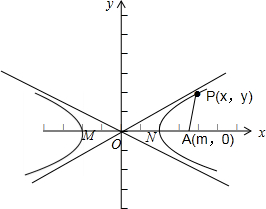
显然,当-2≤m<0时,点A(m,0)到双曲线的左顶点的距离最短,
当0<m≤2时,点A(m,0)到双曲线的右顶点的距离最短,
当m=0时,点A(m,0)到双曲线的左、右顶点的距离相等且最短;
当m>2时,设双曲线右支上任意一点P(x,y),
|PA|2=(x-m)2+y2=(x-m)2+
-1≥|AN|2=(2-m)2,
∴x2-2mx+
-1≥4-4m,
∴(2x-4)m≤
x2-5=
(x2-4),
∵x≥2,
∴m≤
(x+2),又(x+2)min=4,
∴m≤
,
综上,2<m≤
时,点A(m,0)到双曲线的右顶点的距离最短;
同理可得,当-
≤m<-2时,点A(m,0)到双曲线的左顶点的距离最短.
综上所述,当-
≤m≤
时,满足题意.
故选:C.
| x2 |
| 4 |
| 5 |
∴双曲线的左、右顶点分别为为M(-2,0)、N(2,0);

显然,当-2≤m<0时,点A(m,0)到双曲线的左顶点的距离最短,
当0<m≤2时,点A(m,0)到双曲线的右顶点的距离最短,
当m=0时,点A(m,0)到双曲线的左、右顶点的距离相等且最短;
当m>2时,设双曲线右支上任意一点P(x,y),
|PA|2=(x-m)2+y2=(x-m)2+
| x2 |
| 4 |
∴x2-2mx+
| x2 |
| 4 |
∴(2x-4)m≤
| 5 |
| 4 |
| 5 |
| 4 |
∵x≥2,
∴m≤
| 5 |
| 8 |
∴m≤
| 5 |
| 2 |
综上,2<m≤
| 5 |
| 2 |
同理可得,当-
| 5 |
| 2 |
综上所述,当-
| 5 |
| 2 |
| 5 |
| 2 |
故选:C.

练习册系列答案
相关题目