题目内容
9.(1)若x,y都是正实数,且x+y>2,求证:$\frac{1+x}{y}$<2和$\frac{1+y}{x}$<2中至少有一个成立.(2)已知a、b、c∈R+,求证:$\sqrt{\frac{{a}^{2}+{b}^{2}+{c}^{2}}{3}}$≥$\frac{a+b+c}{3}$.
分析 (1)本题证明结论中结构较复杂,而其否定结构简单,故可用反证法证明其否定不成立,以此来证明结论成立.
(2)利用分析法证明即可.
解答 证明:(1)假设$\frac{1+x}{y}$<2和$\frac{1+y}{x}$<2都不成立,即$\frac{1+x}{y}$≥2和$\frac{1+y}{x}$≥2同时成立.…(2分)
∵x>0且y>0,∴1+x≥2y,且1+y≥2x.…(4分)
两式相加得2+x+y≥2x+2y,∴x+y≤2.这与已知条件x+y>2矛盾,
∴$\frac{1+x}{y}$<2和$\frac{1+y}{x}$<2中至少有一个成立. …(6分)
(2)要证$\sqrt{\frac{{a}^{2}+{b}^{2}+{c}^{2}}{3}}$≥$\frac{a+b+c}{3}$,
只需证:3(a2+b2+c2)≥a2+b2+c2+2ab+2bc+2ca,…(9分)
只需证:2(a2+b2+c2)≥2ab+2bc+2ca,…(10分)
只需证:(a-b)2+(b-c)2+(c-a)2≥0,而这是显然成立的,
∴$\sqrt{\frac{{a}^{2}+{b}^{2}+{c}^{2}}{3}}$≥$\frac{a+b+c}{3}$成立 …(12分)
点评 本题考查分析法、反证法证明命题,在作证明题时,对于一些条件相对较少或者证明时需要分类讨论的题型,最好试试用反证法能否证明问题.

练习册系列答案
相关题目
18.使不等式a+b<c+d成立的一个必要不充分条件是( )
| A. | a<c | B. | b<d | C. | a<c或b<d | D. | a<c且b<d |
4.角-1120°是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
19.执行如图所示的程序框图,则输出的结果是( )
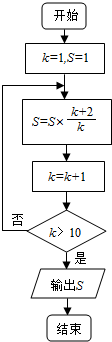

| A. | 9 | B. | 11 | C. | 55 | D. | 66 |