题目内容
设函数f(x)=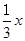 -lnx,则y=f(x)
-lnx,则y=f(x)
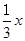 -lnx,则y=f(x)
-lnx,则y=f(x)A.在区间(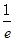 ,1),(1,e)内均有零点 ,1),(1,e)内均有零点 |
B.在区间(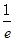 ,1),(1,e)内均无零点 ,1),(1,e)内均无零点 |
C.在区间(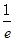 ,1)内有零点,在区间(1,e)内无零点 ,1)内有零点,在区间(1,e)内无零点 |
D.在区间(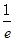 ,1)内无零点,在区间(1,e)内有零点 ,1)内无零点,在区间(1,e)内有零点 |
D
试题分析:先对函数f(x)进行求导,再根据导函数的正负情况判断原函数的增减性可得答案.解:由题得f′(x)=
 ,令f′(x)>0得x>3;令f′(x)<0得0<x<3;f′(x)=0得x=3,故知函数f(x)在区间(0,3)上为减函数,在区间(3,+∞)为增函数,在点x=3处有极小值1-ln3<0;又f(1)=
,令f′(x)>0得x>3;令f′(x)<0得0<x<3;f′(x)=0得x=3,故知函数f(x)在区间(0,3)上为减函数,在区间(3,+∞)为增函数,在点x=3处有极小值1-ln3<0;又f(1)=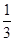 >0,f(e)=
>0,f(e)=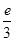 -1<0,f(
-1<0,f(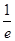 )=
)=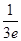 +1>0.故选D.
+1>0.故选D.点评:本题主要考查导函数的增减性与原函数的单调性之间的关系.即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.

练习册系列答案
相关题目
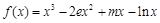 ,记
,记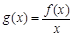 ,若函数
,若函数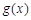 至少存在一个零点,则实数
至少存在一个零点,则实数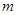 的取值范围是 .
的取值范围是 . 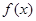 是定义域为R的奇函数,且
是定义域为R的奇函数,且 时,
时,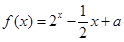 ,则函数
,则函数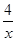 的零点是( )
的零点是( )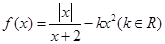 有四个不同的零点,则实数
有四个不同的零点,则实数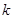 的取值范围是( )
的取值范围是( )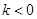
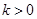
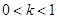
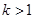
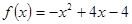 在区间
在区间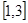 上( )
上( )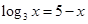 的解所在区间为
的解所在区间为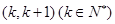 ,则
,则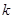 = .
= .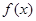 满足
满足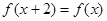 ,且当
,且当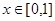 时,
时,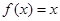 ,则函数
,则函数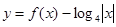 的零点的个数为
的零点的个数为