Question

5．已知直线mx+y+m-1=0上存在点（x，y）满足$\left\{{\begin{array}{l}{x+y-3≤0}\\{x-2y-3≤0}\\{x＞1}\end{array}}\right.$，则实数m的取值范围为（　　）

• A． （-$\frac{1}{2}$，1）
• B． [-$\frac{1}{2}$，1]
• C． （-1，$\frac{1}{2}$）
• D． [-1，$\frac{1}{2}$]

Answer 1

分析 作出不等式组对应的平面区域，利用直线直线mx+y+m-1=0与平面区域的关系，建立条件关系确定m的取值范围．

解答 解：作出不等式组对应的平面区域如图：
直线mx+y+m-1=0等价为y=-m（x+1）+1，则直线过定点D（-1，1），
要使直线mx+y+m-1=0上存在点（x，y）满足$\left\{{\begin{array}{l}{x+y-3≤0}\\{x-2y-3≤0}\\{x＞1}\end{array}}\right.$，
则满足A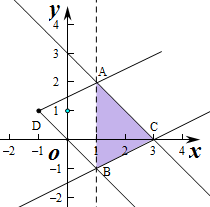在直线mx+y+m-1=0的上方，且B在直线mx+y+m-1=0的下方，
由$\left\{\begin{array}{l}{x=1}\\{x+y-3=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$，即A（1，2），
由$\left\{\begin{array}{l}{x=1}\\{x-2y-3=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$，即B（1，-1），
则满足$\left\{\begin{array}{l}{m+2+m-1＞0}\\{m-1+m-1＜0}\end{array}\right.$，
即$\left\{\begin{array}{l}{m＞-\frac{1}{2}}\\{m＜1}\end{array}\right.$，得-$\frac{1}{2}$＜m＜1，
故选：A

点评 本题考查线性规划知识的运用，考查学生的理解能力，利用数形结合是解决此类问题的基本方法．