题目内容
6.已知圆C的半径为1,圆心C在直线3x-y=0上.(Ⅰ)若圆C被直线x-y+3=0截得的弦长为$\sqrt{2}$,求圆C的标准方程;
(Ⅱ)设点A(0,3),若圆C上总存在两个点到点A的距离为2,求圆心C的横坐标a的取值范围.
分析 (Ⅰ)若圆C被直线x-y+3=0截得的弦长为$\sqrt{2}$,利用勾股定理,即可求圆C的标准方程;
(Ⅱ)由题意,问题等价于圆A和圆C相交时,求圆心C横坐标a的取值范围.
解答 解:(Ⅰ)因为圆心C在直线3x-y=0上,所以设圆心C的坐标为(a,3a),
因为圆C的半径为1,圆C被直线x-y+3=0截得的弦长为$\sqrt{2}$,
所以圆心C到直线x-y+3=0的距离$d=\sqrt{{1^2}-{{({\frac{{\sqrt{2}}}{2}})}^2}}=\frac{{\sqrt{2}}}{2}$,
又$d=\frac{{|{a-3a+3}|}}{{\sqrt{2}}}=\frac{{|{2a-3}|}}{{\sqrt{2}}}$,所以$\frac{{|{2a-3}|}}{{\sqrt{2}}}=\frac{{\sqrt{2}}}{2}$,
解得a=1或a=2,所以圆心C的坐标为(1,3)或(2,6).
所以圆C的标准方程为:(x-1)2+(y-3)2=1或(x-2)2+(y-6)2=1.(6分)
(Ⅱ)设圆A:x2+(y-3)2=4,由(Ⅰ)设圆心C的坐标为(a,3a).
由题意,问题等价于圆A和圆C相交时,求圆心C横坐标a的取值范围,即:$1<\sqrt{{a^2}+{{(3a-3)}^2}}<3$,
由$\sqrt{{a^2}+{{(3a-3)}^2}}>1$整理得5a2-9a+4>0,解得$a<\frac{4}{5}$或a>1;
由$\sqrt{{a^2}+{{(3a-3)}^2}}<3$整理得5a2-9a<0,解得$0<a<\frac{9}{5}$.
所以$0<a<\frac{4}{5}$或$1<a<\frac{9}{5}$.(6分)
点评 本题考查圆的方程的应用,直线与圆的位置关系,考查分析问题解决问题的能力.

 智能训练练测考系列答案
智能训练练测考系列答案| A. | y=2x+1(x>1) | B. | y=x2-x+1 | C. | $y=\frac{1}{x}$ | D. | y=$\frac{1}{{x}^{2}}$ |
| A. | $\frac{5π}{6}$ | B. | $\frac{5π}{3}$ | C. | $\frac{11π}{6}$ | D. | $\frac{2π}{3}$ |
| A. | 最大值1 | B. | 最大值$\frac{3}{2}$ | C. | 最小值$\frac{3}{2}$ | D. | 最小值1 |
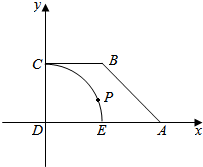 已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=DC=1,以D为圆心,DC为半径,作弧和AD交于点E,点P为劣弧CE上的动点,如图所示.
已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=DC=1,以D为圆心,DC为半径,作弧和AD交于点E,点P为劣弧CE上的动点,如图所示.