Question

【题目】已知M是椭圆C：+=1(a>b>0)上一点，F1F2分别为椭圆C的左右焦点，且|F1F2|=2，∠F1MF2=，△F1MF2的面积为.

（1）求椭圆C的方程；

（2）直线l过椭圆C右焦点F2，交该椭圆于AB两点，AB中点为Q，射线OQ交椭圆于P，记△AOQ的面积为S1，△BPQ的面积为S2，若，求直线l的方程.

Answer 1

【答案】（1）+=1；（2）.

【解析】

（1）根据 |F1F2|=2，得到c=1，设根据∠F1MF2=，△F1MF2的面积为，，得到，然后在中，由余弦定理结合椭圆的定义解得 ，求得即可.

（2）根据，由，得到，从而，当AB斜率不存在时，，不合题意，当AB斜率存在时，设直线方程为，设点，则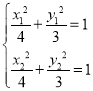，两式作差得到，故设直线OP的方程为：，分别联立椭圆方程和直线AB的方程，求得点P，Q的坐标，由求解.

（1）因为 |F1F2|=2，

所以c=1，设

，

因为∠F1MF2=，△F1MF2的面积为，

所以，

所以，

在中，由余弦定理得：，

即，

解得，

所以，

所以椭圆C的方程是+=1.

（2）因为，

所以，

所以，

所以，

当AB斜率不存在时，，不合题意，

当AB斜率存在时，设直线方程为，

设点，

则，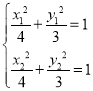

两式作差得：，即，

故直线OP的方程为：，

联立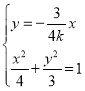，解得，

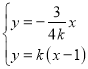联立，解得，

因为，

所以，

即，

解得：，

所以直线AB的方程为.