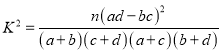题目内容
【题目】已知动圆M与直线
相切，且与定圆C：
外切，
求动圆圆心M的轨迹方程．
求动圆圆心M的轨迹上的点到直线
的最短距离．
【答案】（1）
； （2）
.
【解析】
（1）设动圆圆心为M（x，y），半径为r，题目动点M（x，y）到C（0，﹣3）的距离等于点M到直线y＝3的距离，判断轨迹是抛物线方程，求解即可；
（2）设直线方程为y＝x+m，
，利用判别式为0，求出切线方程，利用平行线之间的距离求解即可．
设动圆圆心为
，半径为r，
由题意知动点到
的距离等于点M到直线
的距离，
由抛物线的定义可知，动圆圆心M的轨迹是以
为焦点，以为准线的一条抛物线，
故所求动圆圆心M的轨迹方程为：
.
（2）设直线方程为y＝x+m，，
可得x2+12x+12m＝0，由△＝122﹣4×12m＝0，
解得m＝3，d
．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
【题目】哈三中群力校区高二、六班同学用随机抽样的办法对所在校区老师的饮食习惯进行了一次调查, 饮食指数结果用茎叶图表示如图, 图中饮食指数低于70的人是饮食以蔬菜为主；饮食指数高于70的人是饮食以肉类为主.
(1)完成下列2×2列联表：
能否有99％的把握认为老师的饮食习惯与年龄有关？
(2)从群力校区任选一名老师, 设“选到45岁以上老师”为事件
, “饮食指数高于70的老师”为事件
, 用调查的结果估计
及
（用最简分数作答）；
(3)为了给食堂提供老师的饮食信息, 根据(1)(2)的结论，能否有更好的抽样方法来估计老师的饮食习惯, 并说明理由.附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
