题目内容
(本小题满分12分)已知椭圆 过点A(a,0),B(0,b)的直
过点A(a,0),B(0,b)的直
线倾斜角为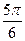 ,原点到该直线的距离为
,原点到该直线的距离为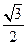 .
.
(1)求椭圆的方程;
(2)斜率小于零的直线过点D(1,0)与椭圆交于M,N两点,若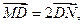 求直线MN的方程;
求直线MN的方程;
(3)是否存在实数k,使直线 交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。
交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。
解:(Ⅰ)由 ,
,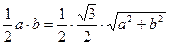 ,得
,得 ,
,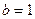 ,
,
所以椭圆方程是: ……………………3分
……………………3分
(Ⅱ)设MN: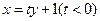 代入
代入 ,得
,得 ,
,
设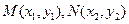 ,由
,由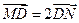 ,得
,得 .
.
由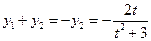 ,
,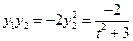 ……………………6分
……………………6分
得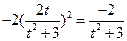 ,
, ,
,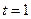 (舍去)
(舍去)
直线 的方程为:
的方程为: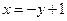 即
即 ……………………8分
……………………8分
(Ⅲ)将 代入
代入 ,得
,得 (*)
(*)
记 ,
,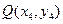 ,
, 为直径的圆过
为直径的圆过 ,则
,则 ,即
,即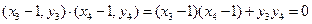 ,又
,又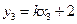 ,
,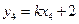 ,得
,得 ………①
………①
又 ,代入①解得
,代入①解得 ……………11分
……………11分
此时(*)方程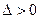 ,
, 存在
存在 ,满足题设条件.…………12分
,满足题设条件.…………12分
解析

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
在极坐标系中,圆ρ=2cos θ的垂直于极轴的两条切线方程分别为( )
| A.θ=0(ρ∈R)和ρcos θ=2 | B.θ=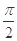 (ρ∈R)和ρcos θ=2 (ρ∈R)和ρcos θ=2 |
C.θ=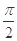 (ρ∈R)和ρcos θ=1 (ρ∈R)和ρcos θ=1 | D.θ=0(ρ∈R)和ρcos θ=1 |
极坐标系中,由三条曲线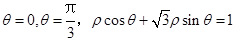 围成的图形的面积是( )
围成的图形的面积是( )
A.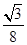 | B.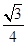 | C.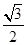 | D.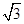 |
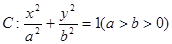 经过点
经过点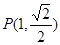 ,且两焦点与短轴的一个端点的连线构成等腰直角三角形.
,且两焦点与短轴的一个端点的连线构成等腰直角三角形.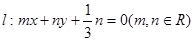 交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T。若存在,求出点T的坐标;若不存在,请说明理由.
交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T。若存在,求出点T的坐标;若不存在,请说明理由.
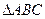 的两个顶点
的两个顶点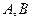 的坐标分别为
的坐标分别为 ,平面内两点
,平面内两点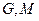 同时满足一下条件:①
同时满足一下条件:①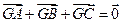 ;②
;②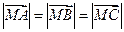 ;③
;③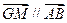
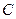 的轨迹方程;
的轨迹方程;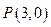 的直线
的直线 与(1)中的轨迹交于
与(1)中的轨迹交于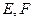 两点,求
两点,求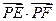 的取值范围。
的取值范围。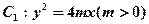 的准线与x轴交于点
的准线与x轴交于点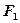 ,
,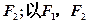 为焦点,离心率为
为焦点,离心率为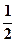 的椭圆
的椭圆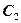 与抛物线
与抛物线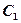 在x轴上方的交点为P
在x轴上方的交点为P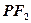 交抛物线于点Q,M是抛物线
交抛物线于点Q,M是抛物线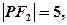 且P点横坐标为
且P点横坐标为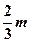 ,求面积
,求面积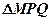 的最大值
的最大值
 =2sin(
=2sin(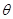 +
+ )的图形是( )
)的图形是( )
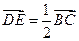 ,求以B,C为焦点且过点D,E的双曲线的离心
,求以B,C为焦点且过点D,E的双曲线的离心