题目内容
(本小题满分12分)已知椭圆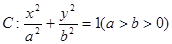 经过点
经过点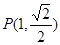 ,且两焦点与短轴的一个端点的连线构成等腰直角三角形.
,且两焦点与短轴的一个端点的连线构成等腰直角三角形.
(1)求椭圆的方程;
(2)动直线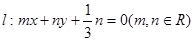 交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T。若存在,求出点T的坐标;若不存在,请说明理由.
交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T。若存在,求出点T的坐标;若不存在,请说明理由.
(1)两焦点与短轴的一个端点的连线构成等腰直角三角形, ,,椭圆
,,椭圆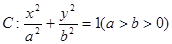 经过点
经过点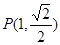 ,代入得
,代入得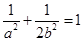 ,得
,得 ,
,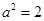
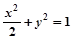 ………………………4分
………………………4分
(2)i)若n=0,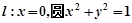
ii)若m=0,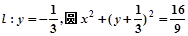 且过定点(0,1)………………………6分
且过定点(0,1)………………………6分
iii)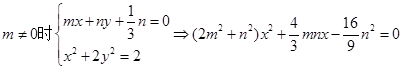
设A(x1,y1),B(x2,y2),则以AB为直径的圆的方程为
(x-x1)(x-x2)+(y-y1)(y-y2)=0 …………………8分
∵
∴圆方程为:
将(0,1)代入显然成立,故存在T(0,1)符合题意。 …………………12分
解析

练习册系列答案
相关题目
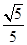 的椭圆
的椭圆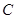 :
: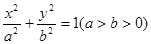 的左、右焦点分别为
的左、右焦点分别为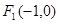 、
、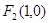 ,
,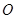 是坐标原点.
是坐标原点.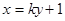 与
与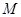 、
、 ,且
,且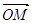

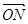
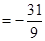 ,求
,求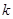 .(其中
.(其中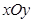 中,
中, 是抛物线
是抛物线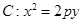
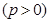 的焦点,
的焦点,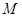 是抛物线
是抛物线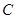 上位于第一象限内的任意一点,过
上位于第一象限内的任意一点,过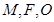 三点的圆的圆心为
三点的圆的圆心为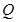 ,点
,点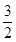 .(Ⅰ)求抛物线
.(Ⅰ)求抛物线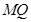 与抛物线
与抛物线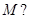 若存在,求出点
若存在,求出点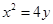 的焦点为
的焦点为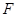 ,过焦点
,过焦点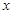 轴的动直线
轴的动直线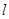 交抛物线于
交抛物线于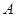 ,
,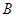 两点,抛物线在
两点,抛物线在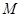 .
.

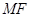 交该抛物线于
交该抛物线于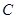 ,
,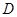 两点,求四边形
两点,求四边形 面积的最小值.
面积的最小值.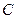 的中心在原点,焦点
的中心在原点,焦点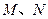 在
在 轴上,且焦距为
轴上,且焦距为 ,实轴长为4
,实轴长为4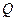 ,使得
,使得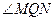 为钝角?若存在,求出点
为钝角?若存在,求出点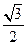 ,已知点P(0,
,已知点P(0,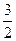 )到这个椭圆上的点的最远距离是
)到这个椭圆上的点的最远距离是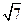 ,求这个椭圆的方程。
,求这个椭圆的方程。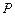 是圆
是圆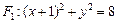 上任意一点,点
上任意一点,点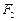 与点
与点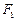 关于原点对称。线段
关于原点对称。线段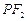 的中垂线
的中垂线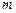 分别与
分别与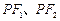 交于
交于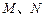 两点.
两点.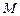 的轨迹
的轨迹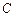 的方程;
的方程; 的直线
的直线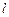 与曲线
与曲线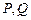 两点,若
两点,若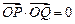 (
(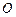 为坐标原点),试求直线
为坐标原点),试求直线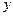 轴
轴 上截距的取值范围.
上截距的取值范围. 过点A(a,0),B(0,b)的直
过点A(a,0),B(0,b)的直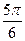 ,原点到该直线的距离为
,原点到该直线的距离为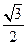 .
.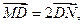 求直线MN的方程;
求直线MN的方程; 交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。
交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。 是双曲线
是双曲线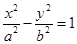 上不同的三点,且
上不同的三点,且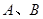 连线经过坐标原点,
连线经过坐标原点, 的斜率乘积
的斜率乘积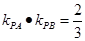 ,求双曲线的离心率;
,求双曲线的离心率;