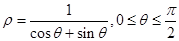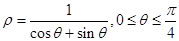题目内容
(本题满分15分)如图,设抛物线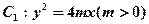 的准线与x轴交于点
的准线与x轴交于点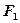 ,
,
焦点为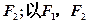 为焦点,离心率为
为焦点,离心率为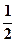 的椭圆
的椭圆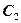 与抛物线
与抛物线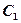 在x轴上方的交点为P
在x轴上方的交点为P
,延长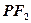 交抛物线于点Q,M是抛物线
交抛物线于点Q,M是抛物线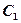 上一动点,且M在P与Q之间运动。
上一动点,且M在P与Q之间运动。
1)当m=3时,求椭圆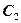 的标准方程;
的标准方程;
2)若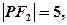 且P点横坐标为
且P点横坐标为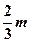 ,求面积
,求面积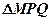 的最大值
的最大值
解:(1)当m=3时, ……………………………………………………1分
……………………………………………………1分
设椭圆方程为
又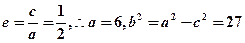
所以椭圆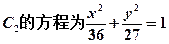 ……………………………………………………4分
……………………………………………………4分
2)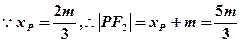
又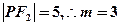
此时抛物线方程为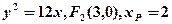 ………………………………………………6分
………………………………………………6分
又P在x轴上方,
∴直线PQ的斜率为: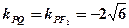
∴直线PQ的方程为: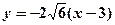 ………………………………………………………8分
………………………………………………………8分
联立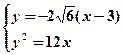 ,得
,得
∵直线PQ的斜率 为
为 ,由图知
,由图知
所以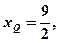 代入抛物线方程得
代入抛物线方程得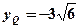 ,即
,即
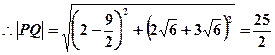
(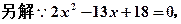

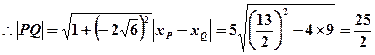 )………………………………11分
)………………………………11分
设点 到直线PQ的距离为d,
到直线PQ的距离为d,
∵M在P与Q之间运动,∴
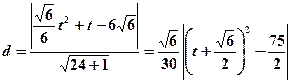 =
=
当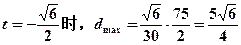 …………………………………………………14分
…………………………………………………14分
即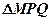 面积的最大值为
面积的最大值为 …………………………………15分
…………………………………15分
解析

练习册系列答案
相关题目
极坐标方程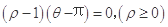 表示的图形是( )
表示的图形是( )
| A.两个圆 | B.一个圆和一条直线 |
| C.一个圆和一条射线 | D.一条直线和一条射线 |
在平面直角坐标系中,曲线C: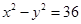 经过伸缩变换
经过伸缩变换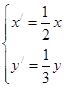 后,所得曲线的焦点坐标为( ).
后,所得曲线的焦点坐标为( ).
A.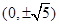 | B.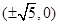 | C.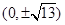 | D.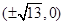 |
极坐标方程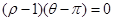
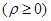 表示的图形是( )
表示的图形是( )
| A.两个圆 | B.两条直线 |
| C.一个圆和一条射线 | D.一条直线和一条射线 |
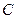 的中心在原点,焦点
的中心在原点,焦点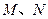 在
在 轴上,且焦距为
轴上,且焦距为 ,实轴长为4
,实轴长为4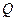 ,使得
,使得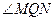 为钝角?若存在,求出点
为钝角?若存在,求出点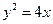 ,
,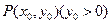 为抛物线上一点
为抛物线上一点 ,
,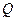 为
为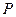 关于
关于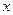 轴对称的点,
轴对称的点,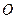 为坐标原点.
为坐标原点.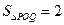 ,求
,求 (1)中的点
(1)中的点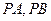 交抛物线
交抛物线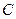 于
于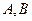 两点, 且斜率分别为
两点, 且斜率分别为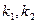 ,且
,且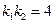 ,求证:直线
,求证:直线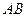 过定点,并求出该定点坐标
过定点,并求出该定点坐标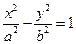 (a>1,b>0)的焦距为2c,直线
(a>1,b>0)的焦距为2c,直线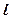 过点(a,0)和(0,b),且点(1,0)到直线
过点(a,0)和(0,b),且点(1,0)到直线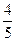 c.求双曲线的离心率e的取值范围.
c.求双曲线的离心率e的取值范围. 过点A(a,0),B(0,b)的直
过点A(a,0),B(0,b)的直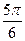 ,原点到该直线的距离为
,原点到该直线的距离为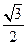 .
.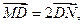 求直线MN的方程;
求直线MN的方程; 交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。
交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。 轴的非负半轴为极轴建立极坐标系,则线段
轴的非负半轴为极轴建立极坐标系,则线段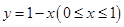 的极坐标为( )
的极坐标为( )