题目内容
已知圆锥母线长为6,底面圆半径长为4,点 是母线
是母线 的中点,
的中点, 是底面圆的直径,底面半径
是底面圆的直径,底面半径 与母线
与母线 所成的角的大小等于
所成的角的大小等于 .
.

(1)当 时,求异面直线
时,求异面直线 与
与 所成的角;
所成的角;
(2)当三棱锥 的体积最大时,求
的体积最大时,求 的值.
的值.
 是母线
是母线 的中点,
的中点, 是底面圆的直径,底面半径
是底面圆的直径,底面半径 与母线
与母线 所成的角的大小等于
所成的角的大小等于 .
.
(1)当
 时,求异面直线
时,求异面直线 与
与 所成的角;
所成的角;(2)当三棱锥
 的体积最大时,求
的体积最大时,求 的值.
的值.(1) 或
或 ,(2)
,(2) .
.
 或
或 ,(2)
,(2) .
.试题分析:(1)求异面直线所成角,关键在平移,即将空间角转化为平面角.利用中位线实现线线之间平移. 连
 ,过
,过 作
作 ,则
,则

 等于异面直线
等于异面直线 与
与 所成的角或其补角.又
所成的角或其补角.又 ,所以
,所以 为异面直线OC与PB所成的角或其补角.明确角之后,只需在相应三角形中求解即可.(2)因为三棱锥
为异面直线OC与PB所成的角或其补角.明确角之后,只需在相应三角形中求解即可.(2)因为三棱锥 的高确定,所以要使得三棱锥
的高确定,所以要使得三棱锥 的体积最大只要底面积
的体积最大只要底面积 的面积最大.而
的面积最大.而 的两边确定为半径,因此要使得
的两边确定为半径,因此要使得 的面积最大,只需两半径夹角的正弦值最大,也即为直角.
的面积最大,只需两半径夹角的正弦值最大,也即为直角.试题解析:解:(1) 连
 ,过
,过 作
作 交
交 于点
于点 ,连
,连 .
.
又
 ,
, .又
.又 .
. ,
,
 等于异面直线
等于异面直线 与
与 所成的角或其补角.
所成的角或其补角.
 ,
,
 或
或 . 5分
. 5分当
 时,
时,
 .
.
 ,
,

当
 时,
时,
 .
.
 ,
,

综上异面直线
 与
与 所成的角等于
所成的角等于 或
或 . 8分
. 8分(2)
 三棱锥
三棱锥 的高为
的高为 且长为
且长为 ,要使得三棱锥
,要使得三棱锥 的体积最大只要底面积
的体积最大只要底面积 的面积最大.而当
的面积最大.而当 时,
时, 的面积最大. 10分
的面积最大. 10分又
 ,此时
,此时 ,
,
 ,
, 12分
12分
练习册系列答案
相关题目
 中,
中, ,
, 分别是
分别是 的中点,且
的中点,且
 .
.
 与
与 所成角的大小;
所成角的大小; 与平面
与平面 所成角的正弦值.
所成角的正弦值. 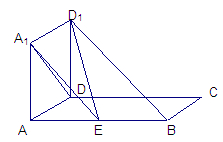
 ?,若存在,求出AM的长,若不存在,说明理由
?,若存在,求出AM的长,若不存在,说明理由 的底面为等腰直角三角形,
的底面为等腰直角三角形, ,
, ,
, 分别是
分别是 的中点。求异面直线
的中点。求异面直线 和
和 所成角的大小。
所成角的大小。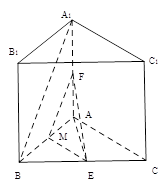




 的棱长均相等,则
的棱长均相等,则 与侧面
与侧面 所成角的正切值为___.
所成角的正切值为___.

