题目内容
【题目】已知动点P与两个定点O(0,0),A(3,0)的距离的比值为2,点P的轨迹为曲线C.
(1)求曲线C的轨迹方程
(2)过点(﹣1,0)作直线与曲线C交于A,B两点,设点M坐标为(4,0),求△ABM面积的最大值.
【答案】(1)![]() ;(2)2
;(2)2
【解析】
(1)设点![]() ,运用两点的距离公式,化简整理可得所求轨迹方程;
,运用两点的距离公式,化简整理可得所求轨迹方程;
(2)由题意可知,直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 方程为
方程为![]() ,求得
,求得![]() 到直线的距离,以及弦长公式,和三角形的面积公式,运用换元法和二次函数的最值可得所求.
到直线的距离,以及弦长公式,和三角形的面积公式,运用换元法和二次函数的最值可得所求.
(1)设点![]() ,
,![]() ,即
,即![]() ,
,
![]() ,即
,即![]() ,
,
![]() 曲线
曲线![]() 的方程为
的方程为![]() .
.
(2)由题意可知,直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 方程为
方程为![]() ,
,
由(1)可知,点![]() 是圆
是圆![]() 的圆心,
的圆心,
点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,由
,由![]() 得
得![]() ,即
,即![]() ,
,
又![]() ,
,
所以 ,
,
令![]() ,所以
,所以![]() ,
,![]() ,
,
则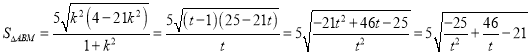 ,
,
所以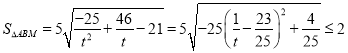 ,
,
当![]() ,即
,即![]() ,此时
,此时![]() ,符合题意,
,符合题意,
即![]() 时取等号,所以
时取等号,所以![]() 面积的最大值为
面积的最大值为![]() .
.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案【题目】高铁、网购、移动支付和共享单车被誉为中国的“新四大发明”,彰显出中国式创新的强劲活力.某移动支付公司从我市移动支付用户中随机抽取100名进行调查,得到如下数据:
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 10 | 8 | 7 | 3 | 2 | 15 |
女 | 5 | 4 | 6 | 4 | 6 | 30 |
合计 | 15 | 12 | 13 | 7 | 8 | 45 |
(Ⅰ)把每周使用移动支付超过3次的用户称为“移动支付活跃用户”,由以上数据完成下列![]() 列联表,并判断能否在犯错误的概率不超过0.005的前提下,认为“移动支付活跃用户”与性别有关?
列联表,并判断能否在犯错误的概率不超过0.005的前提下,认为“移动支付活跃用户”与性别有关?
移动支付活跃用户 | 非移动支付活跃用户 | 总计 | |
男 | |||
女 | |||
总计 | 100 |
(Ⅱ)把每周使用移动支付6次及6次以上的用户称为“移动支付达人”.为了做好调查工作,决定用分层抽样的方法从“移动支付达人”中抽取6人进行问卷调查,再从这6人中选派2人参加活动.求参加活动的2人性别相同的概率?
附公式及表如下:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |


