题目内容
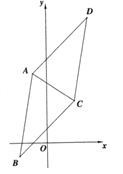
【题目】在直三棱柱ABC—A1B1C1中,∠ACB=90°,AC=2,BC=CC1=![]() ,P是BC1上一动点,则A1P+PC的最小值为_________.
,P是BC1上一动点,则A1P+PC的最小值为_________.
【答案】![]()
【解析】
连A1B,沿BC1将△CBC1展开与△A1BC1在同一个平面内,在BC1上取一点与A1C构成三角形,由三角形两边和大于第三边,得A1P+PC的最小值是A1C的连线.由此利用余弦定理可求解.
连A1B,沿BC1将△CBC1展开与△A1BC1在同一个平面内,
在BC1上取一点与A1C构成三角形,
∵三角形两边和大于第三边,
∴A1P+PC的最小值是A1C的连线.可求解.作展开图:
由∠ACB=90°,AC=2,BC=CC1=![]() ,
,
得AB=![]() =
=![]() ,
,
又AA1=CC1=![]() ,
,
∴A1B=![]() =
=![]() ,BC1=
,BC1=![]() =2,A1C1=AC=2,
=2,A1C1=AC=2,
∴∠A1BC1=45°,∠CBC1=45°,∴∠A1BC=90°,
由余弦定理A1C=![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
【题目】南京市自![]() 年成功创建“国家卫生城市”以来,已经连续三次通过“国家卫生城市”复审,
年成功创建“国家卫生城市”以来,已经连续三次通过“国家卫生城市”复审,![]() 年下半年,南京将迎来第四次复审.为了了解市民绿色出行的意识,现从某单位随机抽取
年下半年,南京将迎来第四次复审.为了了解市民绿色出行的意识,现从某单位随机抽取![]() 名职工,统计了他们一周内路边停车的时间
名职工,统计了他们一周内路边停车的时间![]() (单位:
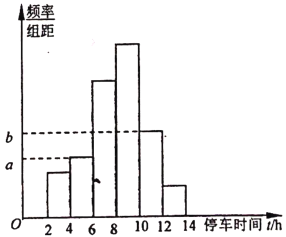
(单位:![]() ),整理得到数据分组及频率分布直方图如下:
),整理得到数据分组及频率分布直方图如下:
组号 | 分组 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)从该单位随机选取一名职工,试估计其在该周内路边停车的时间少于![]() 小时的概率;
小时的概率;
(2)求频率分布直方图中![]() ,
,![]() 的值.
的值.