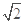题目内容
已知定义在R上的奇函数f(x)和偶函数g(x)满足f(x)+g(x)=ax-a-x+2(a>0且a≠1),若g(2)=a,则f(2)=( ).
| A.2 | B.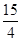 | C.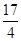 | D.a2 |
B
依题意有f(-2)+g(-2)=-f(2)+g(2)=a-2-a2+2,①
又f(2)+g(2)=a2-a-2+2,②
∴①+②得:2g(2)=2a=4,∴a=2,②-①得:2f(2)=2(a2-a-2),∴f(2)=4-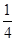 =
=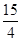
又f(2)+g(2)=a2-a-2+2,②
∴①+②得:2g(2)=2a=4,∴a=2,②-①得:2f(2)=2(a2-a-2),∴f(2)=4-
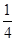 =
=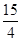

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
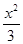 -cos 2x的图像大致是( )
-cos 2x的图像大致是( )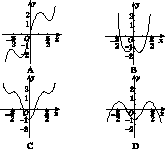
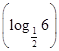 的值是 ( ).
的值是 ( ).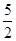
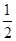
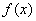 是定义在实数集
是定义在实数集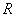 上的以2为周期的偶函数,当
上的以2为周期的偶函数,当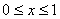 时,
时,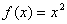 .若直线
.若直线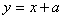 与函数
与函数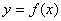 的图像在
的图像在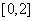 内恰有两个不同的公共点,则实数
内恰有两个不同的公共点,则实数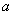 的值是( )
的值是( ) 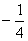 或
或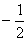 ;
;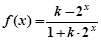 在其定义域上为奇函数,则实数
在其定义域上为奇函数,则实数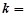 .
.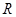 的奇函数
的奇函数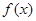 .当
.当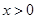 时,
时,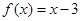 ,则不等式
,则不等式 的解集为( )
的解集为( )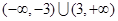
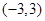
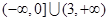
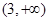
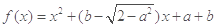 是偶函数,则此函数的图象与y轴交点的纵坐标的最大值为( )
是偶函数,则此函数的图象与y轴交点的纵坐标的最大值为( )