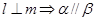题目内容
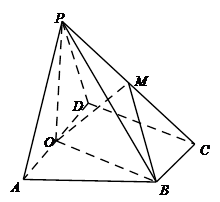
(本题满分15分)如图,在四棱锥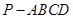 中,底面
中,底面 是矩形,
是矩形,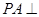 平面
平面 ,
,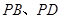 与平面
与平面 所成角的正切值依次是
所成角的正切值依次是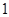 和
和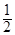 ,
,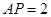 ,
, 依次是
依次是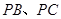 的中点.
的中点.
(Ⅰ)求证: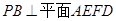 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,底面
中,底面 是矩形,
是矩形,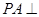 平面
平面 ,
,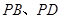 与平面
与平面 所成角的正切值依次是
所成角的正切值依次是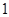 和
和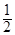 ,
,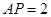 ,
,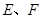 依次是
依次是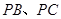 的中点.
的中点.(Ⅰ)求证:
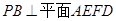 ;
;(Ⅱ)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(1)见解析;(2)直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为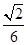 .
.
 与平面
与平面 所成角的正弦值为
所成角的正弦值为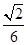 .
. 本试题主要是考查了面面垂直和线面角的求解的综合运用。
(1)第一问中要证明面面垂直关键是证明线面垂直,然后利用判定定理得到。
(2)第二问先根据线面角的定义,作出线面角,然后利用直角三角形的边角的关系求解的得到。
解:(1)∵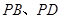 与平面
与平面 所成角的正切值依次
所成角的正切值依次
是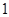 和
和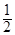 ,
,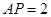 ∴
∴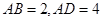
∵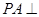 平面
平面 ,底面
,底面 是矩形
是矩形
∴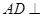 平面
平面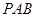 ∴
∴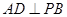
∵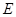 是
是 的中点 ∴
的中点 ∴
∴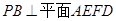 …………………………7分
…………………………7分
(2)解法一:∵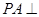 平面
平面 ,∴
,∴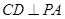 ,又
,又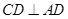 ,
,
∴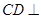 平面
平面 ,取
,取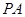 中点
中点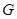 ,
,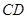 中点
中点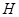 ,联结
,联结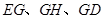 ,
,
则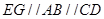 且
且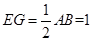 ,
,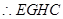 是平行四边形,
是平行四边形,
∴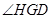 即为直线
即为直线 与平面
与平面 所成的角. 在
所成的角. 在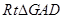 中,,
中,,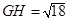 ,
,
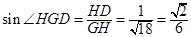 ,
,
∴直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为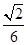 .
.
解法二:分别以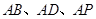 为
为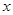 轴、
轴、 轴、
轴、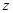 轴建立空间直角坐标系,依题意,
轴建立空间直角坐标系,依题意,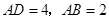 ,则各点坐标分别是
,则各点坐标分别是
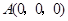 ,
,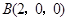 ,
, ,
,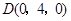 ,
,
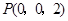 ,∴
,∴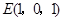 ,
,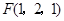 ,
,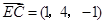 ,
,
又∵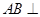 平面
平面 ,
,
∴平面 的法向量为
的法向量为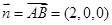 ,
,
设直线 与平面
与平面 所成的角为
所成的角为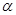 ,则
,则
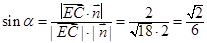 ,
,
∴直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为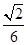 . …………………………15分
. …………………………15分
解:(1)∵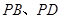 与平面
与平面 所成角的正切值依次
所成角的正切值依次
是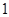 和
和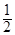 ,
,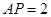 ∴
∴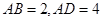
∵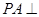 平面
平面 ,底面
,底面 是矩形
是矩形
∴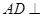 平面
平面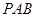 ∴
∴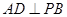
∵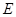 是
是 的中点 ∴
的中点 ∴
∴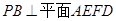 …………………………7分
…………………………7分
(2)解法一:∵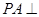 平面
平面 ,∴
,∴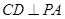 ,又
,又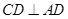 ,
,
∴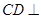 平面
平面 ,取
,取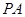 中点
中点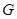 ,
,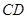 中点
中点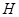 ,联结
,联结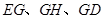 ,
,
则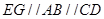 且
且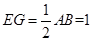 ,
,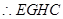 是平行四边形,
是平行四边形,
∴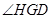 即为直线
即为直线 与平面
与平面 所成的角. 在
所成的角. 在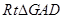 中,,
中,,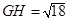 ,
,
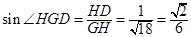 ,
,
∴直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为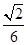 .
.
解法二:分别以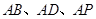 为
为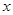 轴、
轴、 轴、
轴、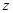 轴建立空间直角坐标系,依题意,
轴建立空间直角坐标系,依题意,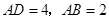 ,则各点坐标分别是
,则各点坐标分别是
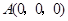 ,
,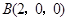 ,
, ,
,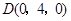 ,
,
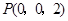 ,∴
,∴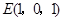 ,
,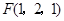 ,
,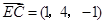 ,
,
又∵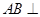 平面
平面 ,
,
∴平面 的法向量为
的法向量为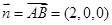 ,
,
设直线 与平面
与平面 所成的角为
所成的角为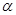 ,则
,则
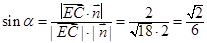 ,
,
∴直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为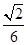 . …………………………15分
. …………………………15分
(1)第一问中要证明面面垂直关键是证明线面垂直,然后利用判定定理得到。
(2)第二问先根据线面角的定义,作出线面角,然后利用直角三角形的边角的关系求解的得到。
解:(1)∵
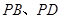 与平面
与平面 所成角的正切值依次
所成角的正切值依次是
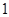 和
和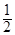 ,
,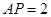 ∴
∴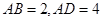
∵
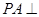 平面
平面 ,底面
,底面 是矩形
是矩形∴
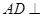 平面
平面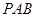 ∴
∴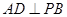
∵
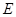 是
是 的中点 ∴
的中点 ∴
∴
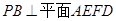 …………………………7分
…………………………7分(2)解法一:∵
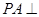 平面
平面 ,∴
,∴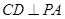 ,又
,又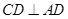 ,
,∴
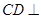 平面
平面 ,取
,取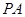 中点
中点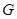 ,
,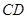 中点
中点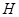 ,联结
,联结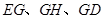 ,
,则
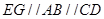 且
且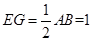 ,
,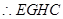 是平行四边形,
是平行四边形,∴
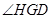 即为直线
即为直线 与平面
与平面 所成的角. 在
所成的角. 在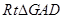 中,,
中,,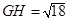 ,
,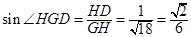 ,
, ∴直线
 与平面
与平面 所成角的正弦值为
所成角的正弦值为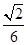 .
. 解法二:分别以
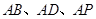 为
为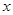 轴、
轴、 轴、
轴、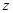 轴建立空间直角坐标系,依题意,
轴建立空间直角坐标系,依题意,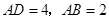 ,则各点坐标分别是
,则各点坐标分别是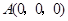 ,
,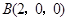 ,
, ,
,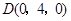 ,
,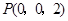 ,∴
,∴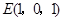 ,
,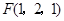 ,
,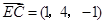 ,
,又∵
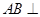 平面
平面 ,
,∴平面
 的法向量为
的法向量为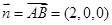 ,
, 设直线
 与平面
与平面 所成的角为
所成的角为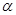 ,则
,则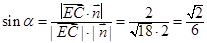 ,
, ∴直线
 与平面
与平面 所成角的正弦值为
所成角的正弦值为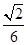 . …………………………15分
. …………………………15分解:(1)∵
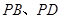 与平面
与平面 所成角的正切值依次
所成角的正切值依次是
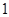 和
和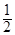 ,
,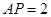 ∴
∴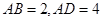
∵
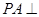 平面
平面 ,底面
,底面 是矩形
是矩形∴
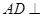 平面
平面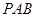 ∴
∴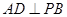
∵
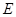 是
是 的中点 ∴
的中点 ∴
∴
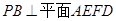 …………………………7分
…………………………7分(2)解法一:∵
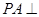 平面
平面 ,∴
,∴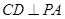 ,又
,又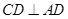 ,
,∴
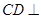 平面
平面 ,取
,取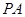 中点
中点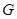 ,
,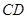 中点
中点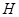 ,联结
,联结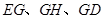 ,
,则
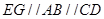 且
且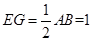 ,
,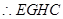 是平行四边形,
是平行四边形,∴
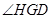 即为直线
即为直线 与平面
与平面 所成的角. 在
所成的角. 在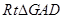 中,,
中,,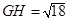 ,
,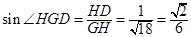 ,
, ∴直线
 与平面
与平面 所成角的正弦值为
所成角的正弦值为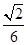 .
. 解法二:分别以
 为
为 轴、
轴、 轴、
轴、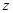 轴建立空间直角坐标系,依题意,
轴建立空间直角坐标系,依题意,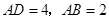 ,则各点坐标分别是
,则各点坐标分别是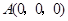 ,
,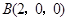 ,
, ,
,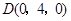 ,
,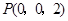 ,∴
,∴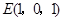 ,
,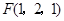 ,
,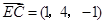 ,
,又∵
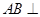 平面
平面 ,
,∴平面
 的法向量为
的法向量为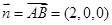 ,
, 设直线
 与平面
与平面 所成的角为
所成的角为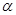 ,则
,则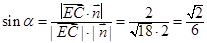 ,
, ∴直线
 与平面
与平面 所成角的正弦值为
所成角的正弦值为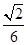 . …………………………15分
. …………………………15分
练习册系列答案
相关题目
 所在的平面与正方形
所在的平面与正方形 所在的平面相互垂直,
所在的平面相互垂直, 、
、 分别是
分别是 、
、 的中点.
的中点.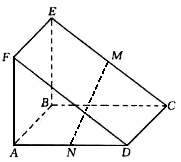
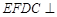 面
面 ;
;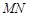 与平面
与平面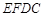 所成的角正弦值.
所成的角正弦值.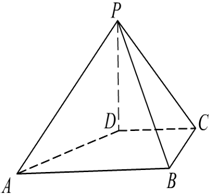
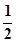 AD=1,CD=
AD=1,CD=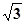 .
.
 ,
, 是底
是底 对角线的交点.
对角线的交点.
 ∥面
∥面 ;
;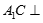 面
面 ,
,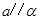 ,
,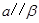 ,则
,则 与
与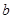 的位置关系是_______.
的位置关系是_______.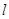 、
、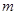 与平面
与平面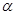 、
、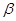 的命题中,正确的是 ( )
的命题中,正确的是 ( )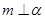 ,
,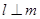 ,则
,则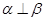 ,
,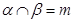 ,
,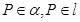 ,且
,且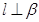
 ,
,
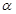 内的一条直线
内的一条直线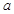 垂直与平面
垂直与平面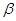 内的无数条直线,则
内的无数条直线,则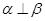
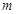 与平面
与平面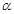 内的一条直线平行,则
内的一条直线平行,则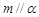
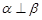 ,且
,且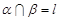 ,则过
,则过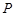 与
与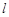 垂直的直线垂直于平面
垂直的直线垂直于平面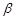
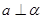 .
.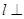 平面
平面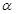 ,直线
,直线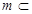 平面
平面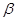 ,则下列四个命题中正确的是 ( )
,则下列四个命题中正确的是 ( )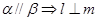 ②
②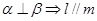 ;③
;③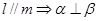 ;④
;④