题目内容
甲、乙、丙三名射击选手,各射击一次,击中目标的概率如下表所示(0<p<1):
若三人各射击一次,恰有k名选手击中目标的概率记为Pk=P(X=k),k=0,1,2,3.
(1)求X的分布列;(2)若击中目标人数的均值是2,求P的值.
| 选手 | 甲 | 乙 | 丙 | ||
| 概率 |
| p | P |
(1)求X的分布列;(2)若击中目标人数的均值是2,求P的值.
(1)由题意得:
P0=
•(1-p)2;
P1=
•(1-p)2+
•p•(1-p)+
•p•(1-p)=-
p2+
,
P2=
•p•(1-p)+
•p•(1-p)+
p2=-
p2+p,
P3=
p2,
∴X的分布列为
…(8分)
(2)EX=0×
•(1-p)2+1×-
p2+
+2×-
p2+p+3×
p2=2p+
,
∴2p+
=2,
∴p=
.…(12分)
P0=
| 1 |
| 2 |
P1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
P2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
P3=
| 1 |
| 2 |
∴X的分布列为
| X | 0 | 1 | 2 | 3 | ||||||||||
| p |
| -
| -
|
|
(2)EX=0×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴2p+
| 1 |
| 2 |
∴p=
| 3 |
| 4 |

练习册系列答案
相关题目
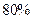 ,计算(结果保留到小数点后面第2位)
,计算(结果保留到小数点后面第2位)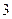 次预报准确的概率
次预报准确的概率 装置就可以正常工作。每套系统都由三种电子模块T1,T2,T3组成(如图所示已知T1,T2,T3正常工作的概率都是
装置就可以正常工作。每套系统都由三种电子模块T1,T2,T3组成(如图所示已知T1,T2,T3正常工作的概率都是 ,且T1,T2,T3能否正常工作相互独立.(注:对每一套系统或每一种电子模块而言,只要有电流通过就能正常工作.)
,且T1,T2,T3能否正常工作相互独立.(注:对每一套系统或每一种电子模块而言,只要有电流通过就能正常工作.)
 ;
; ,求
,求 的分布列和期望.
的分布列和期望. ,乙获胜的概率为
,乙获胜的概率为 .如果将“乙获得冠军”的事件称为“爆出冷门”.试求此项赛事爆出冷门的概率.
.如果将“乙获得冠军”的事件称为“爆出冷门”.试求此项赛事爆出冷门的概率. 服从正态分布
服从正态分布 ,
, ,则
,则 的值等于( )
的值等于( )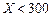
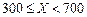
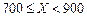
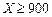
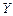
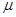 ,
,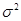 )的随机变量在区间(
)的随机变量在区间(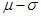 ,
,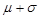 ),(
),(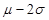 ,
,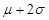 ),和(
),和(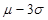 ,
,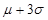 )内取值的概率分别为68.3%,95.4%,和99.7%.某校为高一年级1000名新生每人定制一套校服,经统计,学生的身高(单位:cm)服从正态分布(165,52),则适合身高在155~175cm范围内的校服大约要定制( )
)内取值的概率分别为68.3%,95.4%,和99.7%.某校为高一年级1000名新生每人定制一套校服,经统计,学生的身高(单位:cm)服从正态分布(165,52),则适合身高在155~175cm范围内的校服大约要定制( )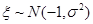 ,且
,且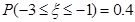 ,则
,则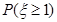 = .
= .