题目内容
如图,给出定点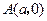
 和直线
和直线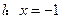 ,
,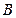 是直线
是直线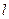 上的动点,
上的动点, 的角平分线交
的角平分线交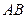 于点
于点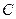 ,求
,求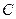 的轨迹方程,并讨论方程表示的曲线类型与
的轨迹方程,并讨论方程表示的曲线类型与 值的关系.
值的关系.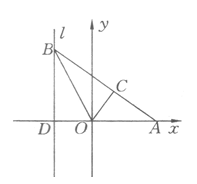
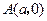
 和直线
和直线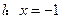 ,
,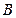 是直线
是直线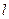 上的动点,
上的动点, 的角平分线交
的角平分线交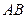 于点
于点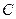 ,求
,求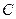 的轨迹方程,并讨论方程表示的曲线类型与
的轨迹方程,并讨论方程表示的曲线类型与 值的关系.
值的关系.
(1)当 时,轨迹方程
时,轨迹方程 ,表示抛物线上的一段弧.
,表示抛物线上的一段弧.
(2)当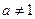 时,轨迹方程为
时,轨迹方程为 . ③
. ③
若 ,方程③表示椭圆上的一段弧;
,方程③表示椭圆上的一段弧;
若 ,方程③表示双曲线上的一段弧.
,方程③表示双曲线上的一段弧.
 时,轨迹方程
时,轨迹方程 ,表示抛物线上的一段弧.
,表示抛物线上的一段弧.(2)当
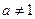 时,轨迹方程为
时,轨迹方程为 . ③
. ③若
 ,方程③表示椭圆上的一段弧;
,方程③表示椭圆上的一段弧;若
 ,方程③表示双曲线上的一段弧.
,方程③表示双曲线上的一段弧.依题意可设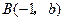 ,
, ,
,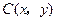 ,
, ,
,
当 时,由
时,由 ,
,
得 ,即
,即 ,
,
化简得 . ①
. ①
又点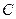 在直线
在直线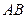 上,则
上,则 . ②
. ②
由式①,②消去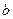 ,得
,得 .
.
当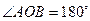 时,
时,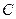 点坐标
点坐标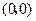 满足上式.
满足上式.
(1)当 时,轨迹方程
时,轨迹方程 ,表示抛物线上的一段弧.
,表示抛物线上的一段弧.
(2)当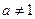 时,轨迹方程为
时,轨迹方程为 . ③
. ③
若 ,方程③表示椭圆上的一段弧;
,方程③表示椭圆上的一段弧;
若 ,方程③表示双曲线上的一段弧.
,方程③表示双曲线上的一段弧.
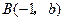 ,
, ,
,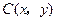 ,
, ,
,当
 时,由
时,由 ,
,得
 ,即
,即 ,
,化简得
 . ①
. ①又点
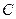 在直线
在直线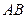 上,则
上,则 . ②
. ②由式①,②消去
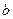 ,得
,得 .
.当
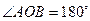 时,
时,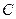 点坐标
点坐标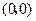 满足上式.
满足上式.(1)当
 时,轨迹方程
时,轨迹方程 ,表示抛物线上的一段弧.
,表示抛物线上的一段弧.(2)当
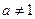 时,轨迹方程为
时,轨迹方程为 . ③
. ③若
 ,方程③表示椭圆上的一段弧;
,方程③表示椭圆上的一段弧;若
 ,方程③表示双曲线上的一段弧.
,方程③表示双曲线上的一段弧.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 和椭圆
和椭圆 有相同的焦点
有相同的焦点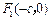 和
和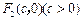 ,两曲线在第一象限内的交点为
,两曲线在第一象限内的交点为 ,椭圆
,椭圆 轴负半轴交于点
轴负半轴交于点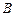 ,且
,且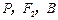 三点共线,
三点共线, 分有向线段
分有向线段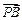 的比为
的比为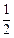 ,又直线
,又直线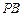 与双曲线
与双曲线 ,若
,若 .
. 与曲线
与曲线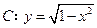 有两个公共点,求实数
有两个公共点,求实数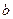 的取值范围.
的取值范围.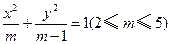 ,过其左焦点且斜率为
,过其左焦点且斜率为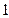 的直线与椭圆及其准线的交点从左到右的顺序为
的直线与椭圆及其准线的交点从左到右的顺序为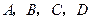 (如图),设
(如图),设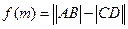 .
.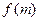 的解析式;
的解析式;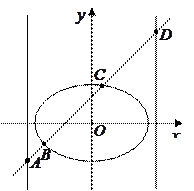
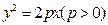 上点
上点 到定点
到定点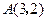 和焦点
和焦点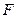 的距离之和的最小值为
的距离之和的最小值为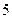 ,求此抛物线的方程.
,求此抛物线的方程. 交双曲线
交双曲线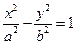 及其渐近线于
及其渐近线于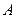 ,
, ,
, ,
, 四点,求证:
四点,求证: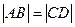 .
.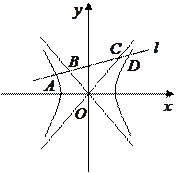
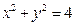 外一点
外一点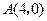 ,作圆的割线,求割线被圆截得的弦的中点的轨迹方程.
,作圆的割线,求割线被圆截得的弦的中点的轨迹方程. 的顶点和准线.
的顶点和准线. 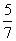 ,求点P到x轴的距离;
,求点P到x轴的距离;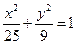 上一点
上一点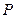 ,它到左准线的距离为
,它到左准线的距离为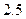 ,求点
,求点