题目内容
16.设函数f(x)=$\frac{x^2}{{1+{x^2}}}$,则.f(2)+f($\frac{1}{2}$)+f(3)+f($\frac{1}{3}$)+…f(10)+f($\frac{1}{10}$)=9.分析 求出f(x)+f($\frac{1}{x}$)的值,然后求解表达式的值即可.
解答 解:函数f(x)=$\frac{x^2}{{1+{x^2}}}$,
f(x)+f($\frac{1}{x}$)=$\frac{{x}^{2}}{1+{x}^{2}}$+$\frac{\frac{1}{{x}^{2}}}{1+\frac{1}{{x}^{2}}}$=$\frac{{x}^{2}}{1+{x}^{2}}+\frac{1}{1+{x}^{2}}$=1.
f(2)+f($\frac{1}{2}$)+f(3)+f($\frac{1}{3}$)+…f(10)+f($\frac{1}{10}$)=9.
故答案为:9.
点评 本题考查函数值的求法,考查计算能力.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
4.复数$\frac{{{{(1+i)}^{10}}}}{1-i}$等于( )
| A. | 16+16i | B. | -16-16i | C. | 16-16i | D. | -16+16i |
1.在△ABC中,内角A、B、C所对的边分别为a、b、c,a=c且满足cosC+(cosA-$\sqrt{3}$sinA)cosB=0,则△ABC是( )
| A. | 钝角三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 不能确定 |
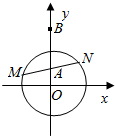 己知圆O:x2十y2=l,及A(0,$\sqrt{2}$-l),B(0,$\sqrt{2}$+l):
己知圆O:x2十y2=l,及A(0,$\sqrt{2}$-l),B(0,$\sqrt{2}$+l):