题目内容
【题目】如图，在四棱锥P－ABCD中，PC⊥底面ABCD，AD∥BC，AD＝2BC＝2，PC＝2，△ABC是以AC为斜边的等腰直角三角形，E是PD的中点．
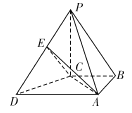
(1)求证：平面EAC⊥平面PCD；
(2)求直线PA与平面EAC所成角的正弦值．
【答案】(1)见解析.
(2) 
.
【解析】分析：（1）推导出
，从而
平面
，由此能证明平面
平面；
（2）作
，则
平面
，从而
与平面所成角
，由此能求出与平面所成角的正弦值．
详解：(1)证明：∵PC⊥底面ABCD，AC底面ABCD，
∴PC⊥AC1分
由题意可知，AD∥BC，且AD＝2BC＝2，
△ABC是等腰直角三角形．
∴AC＝
BC＝，CD＝2分
∴CD2＋AC2＝AD2，即AC⊥CD，3分
又∵PC∩CD＝C4分
∴AC⊥平面PCD5分
∵AC平面EAC
∴平面EAC⊥平面PCD6分
(2)由(1)得平面EAC⊥平面PCD，
平面EAC∩平面PCD＝EC，
作PH⊥EC，∴PH⊥平面EAC8分
所以PA与平面EAC所成角为∠PAH9分
在Rt△PAC中，PA＝
，
在Rt△PHC中，sin∠PCE＝
，PH＝PCsin∠PCE＝
10分
sin∠PAH＝
＝
＝
，所以直线PA与平面EAC所成角的正弦值为12分
练习册系列答案
相关题目
