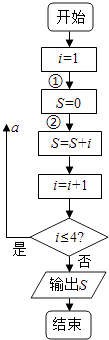
题目内容
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,且它的一个焦点
,且它的一个焦点 ![]() 的坐标为
的坐标为 ![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设过焦点 ![]() 的直线与椭圆相交于
的直线与椭圆相交于 ![]() 两点,
两点, ![]() 是椭圆上不同于
是椭圆上不同于 ![]() 的动点,试求
的动点,试求 ![]() 的面积的最大值.
的面积的最大值.
【答案】解:(Ⅰ)设椭圆的半焦距为 ![]() ,则
,则 ![]() .又由
.又由 ![]() ,可解得
,可解得 ![]() ,
,
所以 ![]() ,
,
所以,椭圆的标准方程为 ![]() .
.
(Ⅱ)设过焦点 ![]() 的直线为
的直线为 ![]() .
.
①若 ![]() 的斜率不存在,则
的斜率不存在,则 ![]() ,即
,即 ![]() ,
,
显然当 ![]() 在短轴顶点
在短轴顶点 ![]() 或
或 ![]() 时,
时, ![]() 的面积最大,
的面积最大,
此时, ![]() 的最大面积为
的最大面积为 ![]() .
.
②若 ![]() 的斜率存在,不妨设为
的斜率存在,不妨设为 ![]() ,则
,则 ![]() 的方程为
的方程为 ![]() .
.
设 ![]() .
.
联立方程: 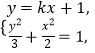 消去
消去 ![]() 整理得:
整理得: ![]() ,
,
所以  则
则 ![]() .
.
因为,当直线与 ![]() 平行且与椭圆相切时,此时切点
平行且与椭圆相切时,此时切点 ![]() 到直线
到直线 ![]() 的距离最大,
的距离最大,
设切线 ![]() ,
,
联立 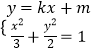 消去y
消去y![]() 整理得:
整理得: ![]() ,
,
由 ![]() ,解得:
,解得: ![]() .
.
又点 ![]() 到直线
到直线 ![]() 的距离
的距离 ![]() ,
,
所以 ![]() ,
,
所以 ![]() .
.
将 ![]() 代入得
代入得 ![]() .
.
令 ![]() ,设函数
,设函数 ![]() ,则
,则 ![]() ,
,
因为当 ![]() 时,
时, ![]() ,当
,当 ![]() 时,
时, ![]() ,
,
所以 ![]() 在
在 ![]() 上是增函数,在
上是增函数,在 ![]() 上是减函数,所以
上是减函数,所以 ![]() .
.
故 ![]() 时,
时, ![]() 面积最大值是
面积最大值是 ![]() .显然
.显然 ![]() ,
,
所以,当 ![]() 的方程为
的方程为 ![]() 时,
时, ![]() 的面积最大,最大值为
的面积最大,最大值为 ![]() .
.
【解析】(1)由条件得到关于a,b,c的方程组求解.
(2)分直线的斜率不存在与存在两种情况讨论,设出直线的方程,代入椭圆方程消去y得关于x的一元二次方程,结合 韦达定理和弦长公式求出弦长,再求出与直线平行的切线方程,由切点到直线的距离不是三角形的高,将三角形的面积表示为m的函数式,先换元,再用导数求出函数的最值.
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目