题目内容
8.已知公差不为零的等差数列{an}的前4项和为10,且a2,a3,a7成等比数列.(Ⅰ)求通项公式an;
(Ⅱ)设bn=$\frac{{a}_{n}+5}{3}$2${\;}^{{a}_{n}+2}$,求数列{bn}的前n项和Sn.
分析 (Ⅰ)设等差数列{an}的公差为d,运用等差数列的通项和求和公式,解方程可得首项和公差d,即可得到通项;
(Ⅱ)化简bn,运用错位相减法,结合等比数列的求和公式,计算即可得到.
解答 解:(Ⅰ)设等差数列{an}的公差为d,
由题意知S4=10,a32=a2a7,
即有$\left\{\begin{array}{l}{4{a}_{1}+6d=10}\\{({a}_{1}+2d)^{2}=({a}_{1}+d)({a}_{1}+6d)}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{a}_{1}=-2}\\{d=3}\end{array}\right.$,
所以an=3n-5.
(Ⅱ)∵bn=$\frac{{a}_{n}+5}{3}$2${\;}^{{a}_{n}+2}$=n•23n-3=n•8n-1,
则Sn=1+2•8+3•82+…+n•8n-1,
所以8Sn=8+2•82+3•83+…+n•8n,
作差得-7Sn=1+8+82+…+8n-1-n•8n=$\frac{1-{8}^{n}}{1-8}$-n•8n,
即有Sn=$\frac{7n•{8}^{n}-{8}^{n}+1}{49}$=$\frac{(7n-1){8}^{n}+1}{49}$.
点评 本题考查等差数列和等比数列的通项和求和公式的运用,同时考查数列求和方法:错位相减法,考查运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.如图是函数y=2sin(ωx+ϕ)(ω>0)图象的一部分,则ω和ϕ为( )
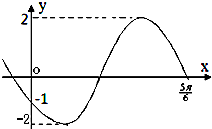

| A. | ω=$\frac{11}{5}$,ϕ=-$\frac{5π}{6}$ | B. | ω=$\frac{7}{5}$,ϕ=-$\frac{π}{6}$ | C. | ω=$\frac{17}{5}$,ϕ=-$\frac{5π}{6}$ | D. | ω=$\frac{13}{5}$,ϕ=-$\frac{π}{6}$ |
18.设F1,F2为椭圆$\frac{x^2}{4}+{y^2}$=1的两个焦点,点P在椭圆上,若线段PF1的中点在y轴上,则$\frac{{|{P{F_2}}|}}{{|{P{F_1}}|}}$的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{7}$ | D. | $\frac{1}{9}$ |