题目内容
(本小题满分12分)
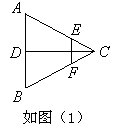
已知如图(1),正三角形ABC的边长为2a,CD是AB边上的高,E、F分别是AC和BC边上的点,且满足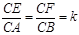 ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
(Ⅰ) 求二面角B-AC-D的大小;
(Ⅱ) 若异面直线AB与DE所成角的余弦值为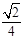 ,求k的值.
,求k的值.
已知如图(1),正三角形ABC的边长为2a,CD是AB边上的高,E、F分别是AC和BC边上的点,且满足
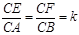 ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2). 
(Ⅰ) 求二面角B-AC-D的大小;
(Ⅱ) 若异面直线AB与DE所成角的余弦值为
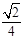 ,求k的值.
,求k的值. (1) 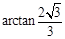 . (2) k=
. (2) k=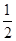
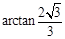 . (2) k=
. (2) k=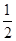
试题分析:解:(Ⅰ) 过D点作DG⊥AC于G,连结BG,
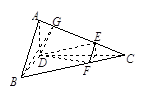
∵ AD⊥CD, BD⊥CD,
∴ ∠ADB是二面角A-CD-B的平面角.
∴ ∠ADB=
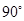 , 即BD⊥AD.
, 即BD⊥AD.∴ BD⊥平面ADC. ∴ BD⊥AC.
∴ AC⊥平面BGD. ∴ BG⊥AC .
∴ ∠BGD是二面角B-AC-D的平面角.
在ADC中,AD=a, DC=
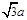 , AC=2a,
, AC=2a,∴
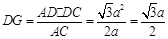 .
.在Rt△BDG中,
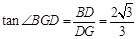 .
.∴
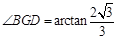 .
.即二面角B-AC-D的大小为
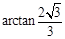 .
. (Ⅱ) ∵ AB∥EF, ∴ ∠DEF(或其补角)是异面直线AB与DE所成的角.
∵
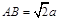 ,∴
,∴ 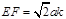 .
.又DC=
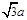 ,
, 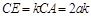 ,
,∴
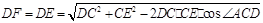
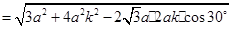
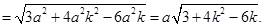
∴
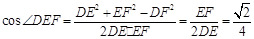 .
.∴
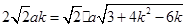 . 解得 k=
. 解得 k=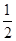 .
.点评:解决该试题的关键是能利用定义求作角,结合三角形来求解得到结论,属于基础题。

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 和直线
和直线 ,给出下列条件:①
,给出下列条件:①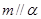 ;②
;②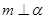 ;③
;③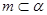 ;④
;④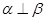 ;⑤
;⑤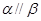 .则使
.则使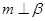 成立的充分条件是 .(填序号)
成立的充分条件是 .(填序号)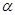 、
、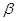 .下列四个命题中,
.下列四个命题中,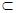
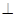
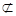
 是两条不同的直线,
是两条不同的直线,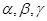 是三个不同的平面,则下列命题中真命题的是( )
是三个不同的平面,则下列命题中真命题的是( ) ,则
,则
 ,则
,则
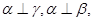 则
则
 ,则
,则
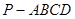 的底面是边长为6的正方形,侧棱
的底面是边长为6的正方形,侧棱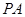 的长为8,且垂直于底面,点
的长为8,且垂直于底面,点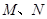 分别是
分别是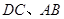 的中点.求
的中点.求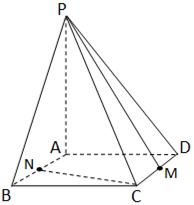
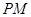 与
与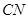 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);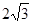 , BC=6.
, BC=6.
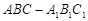 中,△
中,△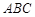 为等腰直角三角形,∠
为等腰直角三角形,∠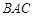 =
=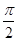 ,且
,且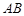 =
=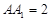 ,
,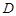 、
、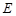 、
、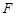 分别为
分别为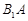 、
、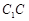 、
、 的中点.
的中点.
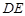 ∥平面
∥平面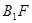 ⊥平面
⊥平面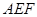 ;
;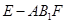 的体积.
的体积.
 、
、 是两条不同的直线,
是两条不同的直线, 、
、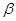 是两个不同的平面,则下列命题中正确的是
是两个不同的平面,则下列命题中正确的是 ,且
,且 ,则
,则
 ,且
,且 ,则
,则
 ,且
,且