题目内容
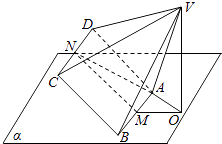
【题目】如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题: ①平面A′FG⊥平面ABC;
②BC∥平面A′DE;
③三棱锥A′﹣DEF的体积最大值为 ![]() a3;
a3;
④动点A′在平面ABC上的射影在线段AF上;
⑤二面角A′﹣DE﹣F大小的范围是[0, ![]() ].
].
其中正确的命题是(写出所有正确命题的编号)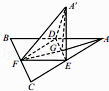
【答案】①②③④
【解析】解:①由已知可得四边形ADEF是菱形,则DE⊥GA′,DE⊥GF, ∴DE⊥平面A′FG,∴平面A′FG⊥平面ABC,①正确;
②由三角形中位线定理可得BC∥DE,∴BC∥平面A′DE,∴②正确;
③当面A′DE⊥面ABC时,三棱锥A′﹣DEF的体积达到最大,
最大值为 ![]() =
= ![]() ,③正确;
,③正确;
④由平面A′FG⊥平面ABC,可知点A′在面ABC上的射影在线段AF上,∴④正确;
⑤在旋转过程中二面角A′﹣DE﹣F大小的范围是[0,π],∴⑤不正确.
故答案为:①②③④.
①由已知可得四边形ADEF是菱形,再利用菱形对角线的性质、线面面面垂直的判定与性质定理即可得出;②由三角形中位线定理和线面平行的判定定理即可得出;③当面A′DE⊥面ABC时,三棱锥A′﹣DEF的体积达到最大,再利用体积计算公式即可得出;④由平面A′FG⊥平面ABC,利用面面垂直的性质定理可得点A′在面ABC上的射影在线段AF上;⑤在旋转过程中二面角A′﹣DE﹣F大小的范围是[0,π],即可判断出.

练习册系列答案
相关题目